6 Logistic regression

Logistic regression is very similar to linear regression, but applied to classification problems. In this chpater our idea is to treat it as the simplest example of a neural network instead of using other methods. The code we developped in the last chapter will be used extensively.

6.1 Basic idea

Assume that we have a binary classfification problem with \(N\) features. Our model starts from the logit instead of the label \(y\) itself.

\[ logit(y)=\theta_0+\sum_{j=1}^N\theta_jx_j. \]

The logit function is used to describe the logorithm of the binary odds. The odd ratio is the ratio between the probability of success and the probability of failure. Assume the probability of success is \(p\). Then

\[ oddratio(p)=\frac{p}{1-p},\quad logit(p)=z = \log\qty(\frac{p}{1-p}). \] We could solve the logit function, and get its inverse: the function is the Sigmoid function. Once we have the logit value, we could use it to get the probability. \[ p=\sigma(z)=\frac{1}{1+\mathrm{e}^{-z}}. \]

Therefore the model for Logistic regression is as follows:

\[ p=\sigma(L(x))=\sigma\left(\theta_0+\sum_{j=1}^n\theta_jx_j\right)=\sigma\left(\Theta \hat{x}^T\right). \]

6.1.1 Sigmoid function

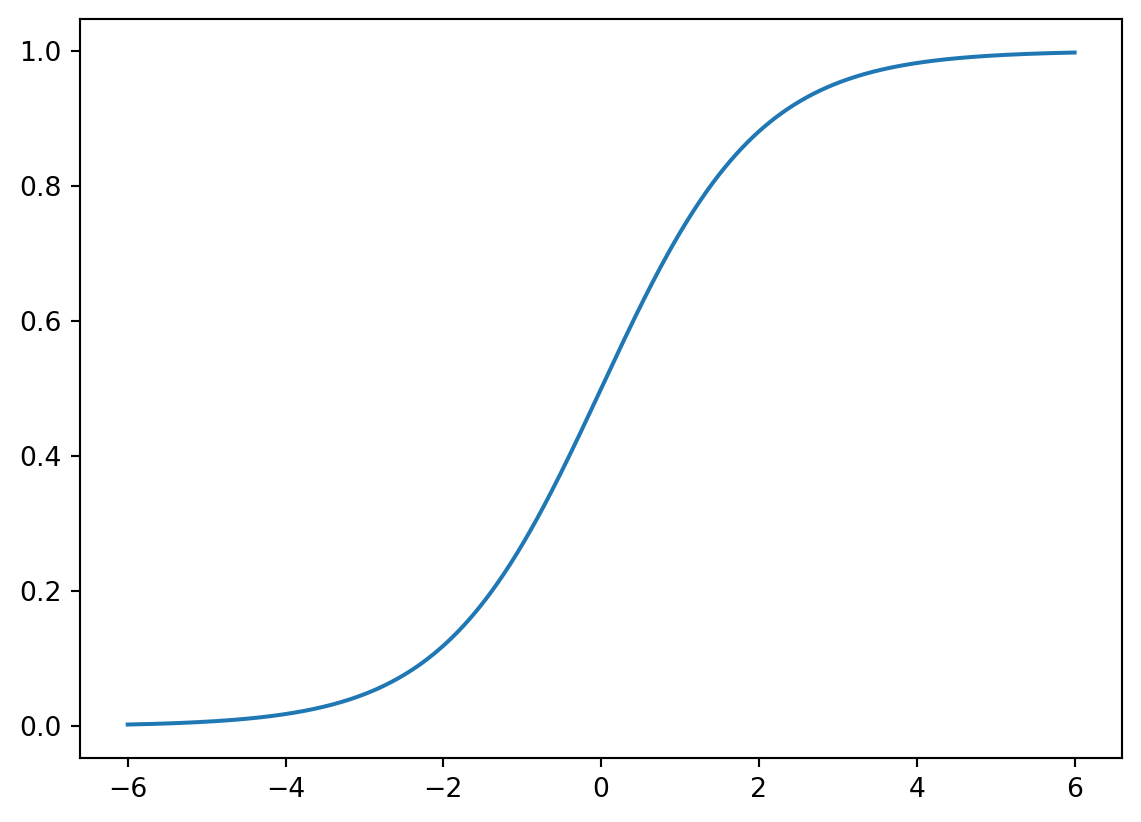
The Sigmoid function is defined as follows:

\[ \sigma(z)=\frac{1}{1+\mathrm{e}^{-z}}. \] The graph of the function is shown below.

The main properties of \(\sigma\) are listed below as a Lemma.

Lemma 6.1 The Sigmoid function \(\sigma(z)\) satisfies the following properties.

\(\sigma(z)\rightarrow \infty\) when \(z\mapsto \infty\).
\(\sigma(z)\rightarrow -\infty\) when \(z\mapsto -\infty\).
\(\sigma(0)=0.5\).
\(\sigma(z)\) is always increasing.
\(\sigma'(z)=\sigma(z)(1-\sigma(z))\).

Solution. We will only look at the last one.

\[ \begin{split} \sigma'(z)&=-\frac{(1+\mathrm e^{-z})'}{(1+\mathrm e^{-z})^2}=\frac{\mathrm e^{-z}}{(1+\mathrm e^{-z})^2}=\frac{1}{1+\mathrm e^{-z}}\frac{\mathrm e^{-z}}{1+\mathrm e^{-z}}\\ &=\sigma(z)\left(\frac{1+\mathrm e^{-z}}{1+\mathrm e^{-z}}-\frac{1}{1+\mathrm e^{-z}}\right)=\sigma(z)(1-\sigma(z)). \end{split} \]

6.1.2 Gradient descent

We would like to use Gradient descent to sovle Logistic regression problems. For binary classification problem, the cost function is defined to be

\[ J(\Theta)=-\frac1m\sum_{i=1}^m\left[y^{(i)}\log(p^{(i)})+(1-y^{(i)})\log(1-p^{(i)})\right]. \] Here \(m\) is the number of data points, \(y^{(i)}\) is the labelled result (which is either \(0\) or \(1\)), \(p^{(i)}\) is the predicted value (which is between \(0\) and \(1\)).

Note

The algorithm gets its name since we are using the gradient to find a direction to lower our height.

6.1.3 The Formulas

Theorem 6.1 The gradient of \(J\) is computed by

\[ \nabla J =\frac1m(\textbf{p}-\textbf{y})^T\hat{\textbf{X}}. \tag{6.1}\]

Click for details.

Proof. The formula is an application of the chain rule for the multivariable functions.

\[ \begin{split} \dfrac{\partial p}{\partial \theta_k}&=\dfrac{\partial}{\partial \theta_k}\sigma\left(\theta_0+\sum_{j=1}^n\theta_jx_j\right)=\dfrac{\partial}{\partial \theta_k}\sigma(L(\Theta))\\ &=\sigma(L)(1-\sigma(L))\dfrac{\partial}{\partial \theta_k}\left(\theta_0+\sum_{j=1}^n\theta_jx_j\right)\\ &=\begin{cases} p(1-p)&\text{ if }k=0,\\ p(1-p)x_k&\text{ otherwise}. \end{cases} \end{split} \] Then

\[ \nabla p = \left(\frac{\partial p}{\partial\theta_0},\ldots,\frac{\partial p}{\partial\theta_n}\right) = p(1-p)\hat{x}. \]

Then

\[ \nabla \log(p) = \frac{\nabla p}p =\frac{p(1-p)\hat{x}}{p}=(1-p)\hat{x}. \]

\[ \nabla \log(1-p) = \frac{-\nabla p}{1-p} =-\frac{p(1-p)\hat{x}}{1-p}=-p\hat{x}. \]

Then

\[ \begin{split} \nabla J& = -\frac1m\sum_{i=1}^m\left[y^{(i)}\nabla \log(p^{(i)})+(1-y^{(i)})\nabla \log(1-p^{(i)})\right]\\ &=-\frac1m\sum_{i=1}^m\left[y^{(i)}(1-p^{(i)})\hat{x}^{(i)}+(1-y^{(i)})(-p^{(i)}\hat{x}^{(i)})\right]\\ &=-\frac1m\sum_{i=1}^m\left[(y^{(i)}-p^{(i)})\hat{x}^{(i)}\right]. \end{split} \]

We write \(\hat{x}^{(i)}\) as row vectors, and stack all these row vectors vertically. What we get is a matrix \(\hat{\textbf X}\) of the size \(m\times (1+n)\). We stack all \(y^{(i)}\) (resp. \(p^{(i)}\)) vectically to get the \(m\)-dim column vector \(\textbf y\) (resp. \(\textbf p\)).

Using this notation, the previous formula becomes

\[ \nabla J =\frac1m(\textbf{p}-\textbf{y})^T\hat{\textbf{X}}. \]

After the gradient can be computed, we can start to use the gradient descent method. Note that, although \(\Theta\) are not explicitly presented in the formula of \(\nabla J\), this is used to modify \(\Theta\):

\[ \Theta_{s+1} = \Theta_s - \alpha\nabla J. \]

Note

If you directly use library, like sklearn or PyTorch, they will handle the concrete computation of these gradients.

6.2 Regularization

6.2.1 Three types of errors

Every estimator has its advantages and drawbacks. Its generalization error can be decomposed in terms of bias, variance and noise. The bias of an estimator is its average error for different training sets. The variance of an estimator indicates how sensitive it is to varying training sets. Noise is a property of the data.

6.2.2 Underfit vs Overfit

When fit a model to data, it is highly possible that the model is underfit or overfit.

Roughly speaking, underfit means the model is not sufficient to fit the training samples, and overfit means that the models learns too many noise from the data. In many cases, high bias is related to underfit, and high variance is related to overfit.

The following example is from the sklearn guide. Although it is a polynomial regression example, it grasps the key idea of underfit and overfit.

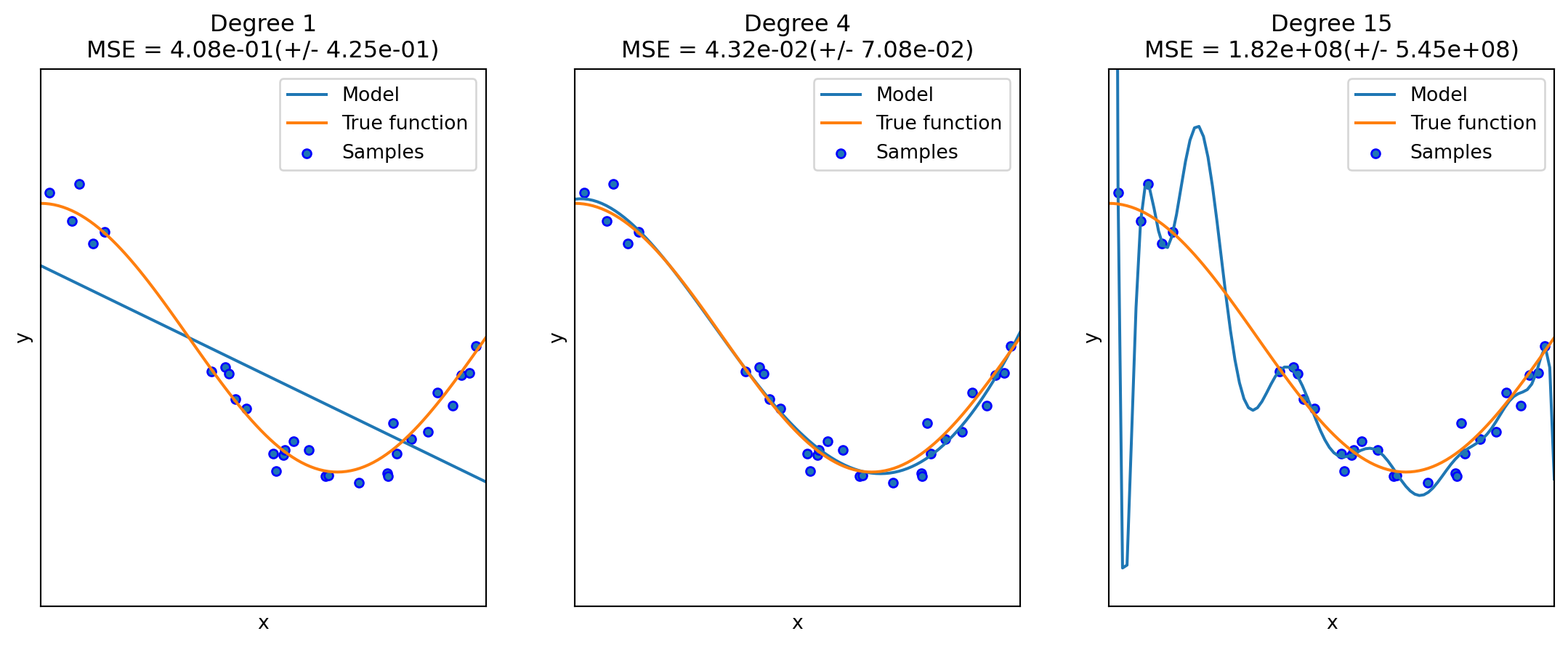
6.2.3 Learning curves (accuracy vs training size)

A learning curve shows the validation and training score of an estimator for varying a key hyperparameter. In most cases the key hyperparameter is the training size or the number of epochs. It is a tool to find out how much we benefit from altering the hyperparameter by training more data or training for more epochs, and whether the estimator suffers more from a variance error or a bias error.

sklearn provides sklearn.model_selection.learning_curve() to generate the values that are required to plot such a learning curve. However this function is just related to the sample size. If we would like to talk about epochs, we need other packages.

Let us first look at the learning curve about sample size. The official document page is here. The function takes input estimator, dataset X, y, and an arry-like argument train_sizes. The dataset (X, y) will be split into pieces using the cross-validation technique. The number of pieces is set by the argument cv. The default value is cv=5. For details about cross-validation please see Section 2.2.5.

Then the model is trained over a random sample of the training set, and evaluate the score over the test set. The size of the sample of the training set is set by the argument train_sizes. This argument is array-like. Therefore the process will be repeated several times, and we can see the impact of increasing the training size.

The output contains three pieces. The first is train_sizes_abs which is the number of elements in each training set. This output is mainly for reference. The difference between the output and the input train_sizes is that the input can be float which represents the percentagy. The output is always the exact number of elements.

The second output is train_scores and the third is test_scores, both of which are the scores we get from the training and testing process. Note that both are 2D numpy arrays, of the size (number of different sizes, cv). Each row is a 1D numpy array representing the cross-validation scores, which is corresponding to a train size. If we want the mean as the cross-validation score, we could use train_scores.mean(axis=1).

After understanding the input and output, we could plot the learning curve. We still use the horse colic as the example. The details about the dataset can be found here.

import pandas as pd
import numpy as np

url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/horse-colic/horse-colic.data'
df = pd.read_csv(url, delim_whitespace=True, header=None)
df = df.replace("?", np.NaN)

df.fillna(0, inplace=True)
df.drop(columns=[2, 24, 25, 26, 27], inplace=True)
df[23].replace({1: 1, 2: 0}, inplace=True)
X = df.iloc[:, :-1].to_numpy().astype(float)
y = df[23].to_numpy().astype(int)

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=42)

C:\Users\Xinli\AppData\Local\Temp\ipykernel_32684\73942173.py:5: FutureWarning: The 'delim_whitespace' keyword in pd.read_csv is deprecated and will be removed in a future version. Use ``sep='\s+'`` instead
  df = pd.read_csv(url, delim_whitespace=True, header=None)
C:\Users\Xinli\AppData\Local\Temp\ipykernel_32684\73942173.py:10: FutureWarning: A value is trying to be set on a copy of a DataFrame or Series through chained assignment using an inplace method.
The behavior will change in pandas 3.0. This inplace method will never work because the intermediate object on which we are setting values always behaves as a copy.

For example, when doing 'df[col].method(value, inplace=True)', try using 'df.method({col: value}, inplace=True)' or df[col] = df[col].method(value) instead, to perform the operation inplace on the original object.


  df[23].replace({1: 1, 2: 0}, inplace=True)

We use the model LogisticRegression. The following code plot the learning curve for this model.

from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline

clf = LogisticRegression(max_iter=1000)
steps = [('scalar', MinMaxScaler()),
         ('log', clf)]
pipe = Pipeline(steps=steps)
from sklearn.model_selection import learning_curve
import numpy as np
train_sizes, train_scores, test_scores = learning_curve(pipe, X_train, y_train,
                                                        train_sizes=np.linspace(0.1, 1, 20))

import matplotlib.pyplot as plt
plt.plot(train_sizes, train_scores.mean(axis=1), label='train')
plt.plot(train_sizes, test_scores.mean(axis=1), label='test')
plt.legend()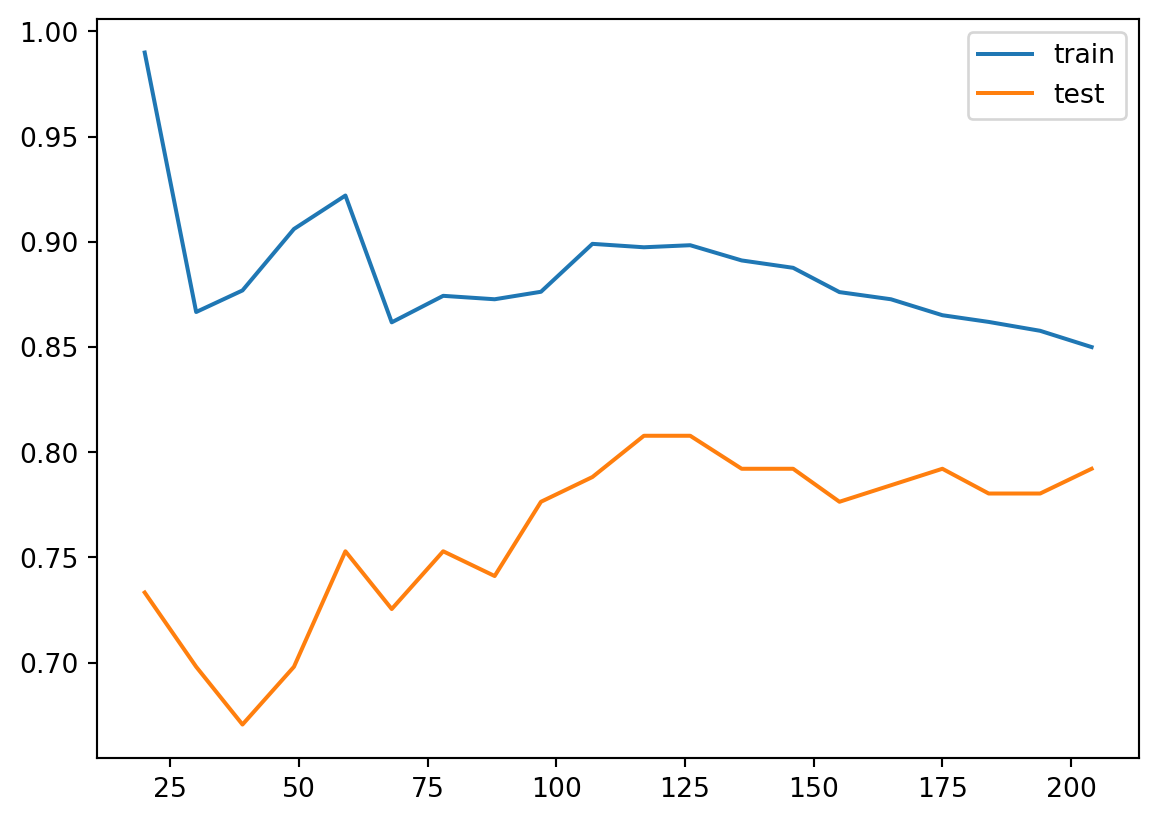

The learning curve is a primary tool for us to study the bias and variance. Usually

If the two training curve and the testing curve are very close to each other, this means that the variance is low. Otherwise the variance is high, and this means that the model probabily suffer from overfitting.
If the absolute training curve score is high, this means that the bias is low. Otherwise the bias is high, and this means that the model probabily suffer from underfitting.

In the above example, although regularization is applied by default, you may still notice some overfitting there.

6.2.4 Regularization

Regularization is a technique to deal with overfitting. Here we only talk about the simplest method: ridge regression, also known as Tikhonov regularizaiton. Because of the formula given below, it is also called \(L_2\) regularization. The idea is to add an additional term \(\dfrac{\alpha}{2m}\sum_{i=1}^m\theta_i^2\) to the original cost function. When training with the new cost function, this additional term will force the parameters in the original term to be as small as possible. After finishing training, the additional term will be dropped, and we use the original cost function for validation and testing. Note that in the additional term \(\theta_0\) is not presented.

The hyperparameter \(\alpha\) is the regularization strength. If \(\alpha=0\), the new cost function becomes the original one; If \(\alpha\) is very large, the additional term dominates, and it will force all parameters to be almost \(0\). In different context, the regularization strength is also given by \(C=\dfrac{1}{2\alpha}\), called inverse of regularization strength.

6.2.4.1 The math of regularization

Theorem 6.2 The gradient of the ridge regression cost function is

\[ \nabla J=\frac1m(\textbf{p}-\textbf{y})^T\hat{\textbf{X}}+\frac{\alpha}{m}\Theta. \]

Note that \(\Theta\) doesn’t contain \(\theta_0\), or you may treat \(\theta_0=0\).

The computation is straightforward.

6.2.4.2 The code

Regularization is directly provided by the logistic regression functions.

In LogisticRegression, the regularization is given by the argument penalty and C. penalty specifies the regularizaiton method. It is l2 by default, which is the method above. C is the inverse of regularization strength, whose default value is 1.
In SGDClassifier, the regularization is given by the argument penalty and alpha. penalty is the same as that in LogisticRegression, and alpha is the regularization strength, whose default value is 0.0001.

Let us see the above example.

clf = LogisticRegression(max_iter=1000, C=0.1)
steps = [('scalar', MinMaxScaler()),
         ('log', clf)]
pipe = Pipeline(steps=steps)
from sklearn.model_selection import learning_curve
import numpy as np
train_sizes, train_scores, test_scores = learning_curve(pipe, X_train, y_train,
                                                        train_sizes=np.linspace(0.1, 1, 20))

import matplotlib.pyplot as plt
plt.plot(train_sizes, train_scores.mean(axis=1), label='train')
plt.plot(train_sizes, test_scores.mean(axis=1), label='test')
plt.legend()

After we reduce C from 1 to 0.1, the regularization strength is increased. Then you may find that the gap between the two curves are reduced. However the overall performace is also reduced, from 85%~90% in C=1 case to around 80% in C=0.1 case. This means that the model doesn’t fit the data well as the previous one. Therefore this is a trade-off: decrease the variance but increase the bias.

6.3 Neural network implement of Logistic regression

In the previous sections, we use gradient descent to run the Logistic regression model. We mentioned some important concepts, like epochs, mini-batch, etc.. We are going to use PyTorch to implement it. We will reuse many codes we wrote in the previous chapter.

6.3.1 Example

We still use the horse colic dataset as an example. We first prepare the dataset.

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split

url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/horse-colic/horse-colic.data'
df = pd.read_csv(url, sep='\\s+', header=None)
df = df.replace("?", np.NaN)

df.fillna(0, inplace=True)
df = df.drop(columns=[2, 24, 25, 26, 27])
df[23] = df[23].replace({1: 1, 2: 0})
X = df.iloc[:, :-1].to_numpy().astype(float)
y = df[23].to_numpy().astype(int)

SEED = 42
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=SEED)

We need to perform normalization before throwing the data into the model. Here we use the MinMaxScaler() from sklearn package.

from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler()
X_train = mms.fit_transform(X_train, y_train)
X_test = mms.transform(X_test)

Then we write a Dataset class to build the dataset and create the dataloaders. Since the set is already split, we don’t need to random_split here.

import torch
from torch.utils.data import Dataset, DataLoader

class MyData(Dataset):
    def __init__(self, X, y):
        self.X = torch.tensor(X, dtype=float)
        self.y = torch.tensor(y, dtype=float).reshape(-1, 1)

    def __getitem__(self, index):
        return (self.X[index], self.y[index])

    def __len__(self):
        return len(self.y)


train_set = MyData(X_train, y_train)
val_set = MyData(X_test, y_test)

train_loader = DataLoader(train_set, batch_size=32, shuffle=True)
val_loader = DataLoader(val_set, batch_size=32)

In the following code, we first set up the original model.

import torch.nn as nn
from torch.nn.modules import Linear

class LoR(nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super().__init__(*args, **kwargs)
        self.linear = Linear(in_features=22, out_features=1, dtype=float)
        self.activation = nn.Sigmoid()

    def forward(self, X):
        # pred = self.activation(self.linear(X))
        pred = self.linear(X)
        # return (pred >= 0).float()
        return pred

Then we derive the base ModelTemplate class.

class LoRModel(ModelTemplate):
    def __init__(self, model, loss_fn, optimizer):
        super().__init__(model, loss_fn, optimizer)
        self.stats['acc_train'] = []
        self.stats['acc_val'] = []

    def compute_acc(self, dataloader):
        with torch.no_grad():
            acc = []
            for X_batch, y_batch in dataloader:
                yhat = torch.sigmoid(self.model(X_batch))
                y_pred = (yhat>=0.5).to(float)
                acc.append((y_pred==y_batch).sum().item())
            # print(acc_train)
        return np.sum(acc)/len(dataloader.dataset)

    def log_update(self, train_time, loss, val_time, val_loss, train_loader, val_loader):
        super().log_update(train_time, loss, val_time, val_loss, train_loader, val_loader)
        acc_train = self.compute_acc(train_loader)
        acc_val = self.compute_acc(val_loader)
        self.stats['acc_train'].append(acc_train)
        self.stats['acc_val'].append(acc_val)


        # p = self.model.state_dict()
        # self.stats['acc'].append([p['linear.bias'].item(), p['linear.weight'].item()])

    def log_output(self, verbose=0):
        s = super().log_output(verbose=0, formatstr=':.6f')
        s.append(f'acc_train: {self.stats['acc_train'][-1]:.6f}')
        s.append(f'acc_val: {self.stats['acc_val'][-1]:.6f}')
        # s.append(f'p: [{self.stats['p'][-1][0]:.6f}, {self.stats['p'][-1][1]:.6f}]')
        if verbose == 1:
            print(' '.join(s))
        return s

from torch.optim import SGD
from torch.nn import BCEWithLogitsLoss, BCELoss

original_model = LoR()
model = LoRModel(model=original_model, loss_fn=BCEWithLogitsLoss(),
                 optimizer=SGD(original_model.parameters(), lr = 0.1))

model.train(train_loader, val_loader, epoch_num=100, verbose=1)

epoch 1 train_time: 0.012002 loss: 0.660165 val_time: 0.000999 val_loss: 0.586527 acc_train: 0.631373 acc_val: 0.711111
epoch 2 train_time: 0.007004 loss: 0.632877 val_time: 0.002000 val_loss: 0.574789 acc_train: 0.639216 acc_val: 0.711111
epoch 3 train_time: 0.006922 loss: 0.618968 val_time: 0.000000 val_loss: 0.557177 acc_train: 0.635294 acc_val: 0.711111
epoch 4 train_time: 0.007000 loss: 0.608678 val_time: 0.001000 val_loss: 0.550046 acc_train: 0.647059 acc_val: 0.711111
epoch 5 train_time: 0.008202 loss: 0.600945 val_time: 0.000949 val_loss: 0.543118 acc_train: 0.635294 acc_val: 0.711111
epoch 6 train_time: 0.008081 loss: 0.593400 val_time: 0.001000 val_loss: 0.537980 acc_train: 0.654902 acc_val: 0.711111
epoch 7 train_time: 0.006731 loss: 0.585208 val_time: 0.002093 val_loss: 0.536863 acc_train: 0.674510 acc_val: 0.733333
epoch 8 train_time: 0.007899 loss: 0.577833 val_time: 0.000999 val_loss: 0.532986 acc_train: 0.690196 acc_val: 0.733333
epoch 9 train_time: 0.005000 loss: 0.572980 val_time: 0.001001 val_loss: 0.532861 acc_train: 0.717647 acc_val: 0.711111
epoch 10 train_time: 0.006002 loss: 0.566206 val_time: 0.001001 val_loss: 0.527841 acc_train: 0.713725 acc_val: 0.711111
epoch 11 train_time: 0.007473 loss: 0.560728 val_time: 0.000997 val_loss: 0.522415 acc_train: 0.717647 acc_val: 0.711111
epoch 12 train_time: 0.008002 loss: 0.555968 val_time: 0.000998 val_loss: 0.519069 acc_train: 0.717647 acc_val: 0.711111
epoch 13 train_time: 0.007010 loss: 0.551708 val_time: 0.002008 val_loss: 0.519409 acc_train: 0.745098 acc_val: 0.711111
epoch 14 train_time: 0.007998 loss: 0.547372 val_time: 0.002002 val_loss: 0.519123 acc_train: 0.752941 acc_val: 0.733333
epoch 15 train_time: 0.005991 loss: 0.544968 val_time: 0.000000 val_loss: 0.515328 acc_train: 0.752941 acc_val: 0.733333
epoch 16 train_time: 0.007001 loss: 0.538719 val_time: 0.001002 val_loss: 0.512927 acc_train: 0.756863 acc_val: 0.755556
epoch 17 train_time: 0.006999 loss: 0.535396 val_time: 0.001000 val_loss: 0.510180 acc_train: 0.760784 acc_val: 0.755556
epoch 18 train_time: 0.008028 loss: 0.531635 val_time: 0.000990 val_loss: 0.509192 acc_train: 0.760784 acc_val: 0.755556
epoch 19 train_time: 0.009000 loss: 0.528633 val_time: 0.001999 val_loss: 0.508492 acc_train: 0.768627 acc_val: 0.755556
epoch 20 train_time: 0.008018 loss: 0.524708 val_time: 0.001412 val_loss: 0.507157 acc_train: 0.764706 acc_val: 0.777778
epoch 21 train_time: 0.008515 loss: 0.521868 val_time: 0.001011 val_loss: 0.504501 acc_train: 0.768627 acc_val: 0.777778
epoch 22 train_time: 0.007004 loss: 0.518677 val_time: 0.001000 val_loss: 0.501269 acc_train: 0.772549 acc_val: 0.777778
epoch 23 train_time: 0.005998 loss: 0.516936 val_time: 0.000000 val_loss: 0.505148 acc_train: 0.772549 acc_val: 0.777778
epoch 24 train_time: 0.006999 loss: 0.513643 val_time: 0.000000 val_loss: 0.501260 acc_train: 0.772549 acc_val: 0.777778
epoch 25 train_time: 0.006999 loss: 0.511099 val_time: 0.001005 val_loss: 0.498737 acc_train: 0.780392 acc_val: 0.777778
epoch 26 train_time: 0.007002 loss: 0.509501 val_time: 0.001001 val_loss: 0.500423 acc_train: 0.780392 acc_val: 0.777778
epoch 27 train_time: 0.007017 loss: 0.505988 val_time: 0.001982 val_loss: 0.500657 acc_train: 0.780392 acc_val: 0.777778
epoch 28 train_time: 0.005007 loss: 0.504516 val_time: 0.000999 val_loss: 0.495599 acc_train: 0.780392 acc_val: 0.777778
epoch 29 train_time: 0.008042 loss: 0.501767 val_time: 0.000999 val_loss: 0.497422 acc_train: 0.780392 acc_val: 0.777778
epoch 30 train_time: 0.006001 loss: 0.499805 val_time: 0.001000 val_loss: 0.494277 acc_train: 0.784314 acc_val: 0.777778
epoch 31 train_time: 0.005997 loss: 0.498464 val_time: 0.001000 val_loss: 0.496333 acc_train: 0.780392 acc_val: 0.755556
epoch 32 train_time: 0.008000 loss: 0.495356 val_time: 0.000985 val_loss: 0.490543 acc_train: 0.784314 acc_val: 0.777778
epoch 33 train_time: 0.006019 loss: 0.494053 val_time: 0.001000 val_loss: 0.492300 acc_train: 0.788235 acc_val: 0.755556
epoch 34 train_time: 0.007984 loss: 0.491240 val_time: 0.000999 val_loss: 0.492885 acc_train: 0.776471 acc_val: 0.755556
epoch 35 train_time: 0.007014 loss: 0.490160 val_time: 0.001991 val_loss: 0.491413 acc_train: 0.776471 acc_val: 0.755556
epoch 36 train_time: 0.017107 loss: 0.488223 val_time: 0.004009 val_loss: 0.493107 acc_train: 0.772549 acc_val: 0.777778
epoch 37 train_time: 0.006999 loss: 0.485914 val_time: 0.002000 val_loss: 0.490898 acc_train: 0.776471 acc_val: 0.777778
epoch 38 train_time: 0.009995 loss: 0.484564 val_time: 0.001000 val_loss: 0.490955 acc_train: 0.772549 acc_val: 0.777778
epoch 39 train_time: 0.009002 loss: 0.482808 val_time: 0.000999 val_loss: 0.489583 acc_train: 0.776471 acc_val: 0.777778
epoch 40 train_time: 0.009010 loss: 0.481539 val_time: 0.000999 val_loss: 0.487595 acc_train: 0.776471 acc_val: 0.777778
epoch 41 train_time: 0.007074 loss: 0.480344 val_time: 0.002008 val_loss: 0.489404 acc_train: 0.780392 acc_val: 0.800000
epoch 42 train_time: 0.008464 loss: 0.478523 val_time: 0.001641 val_loss: 0.488327 acc_train: 0.784314 acc_val: 0.800000
epoch 43 train_time: 0.008202 loss: 0.476778 val_time: 0.001057 val_loss: 0.490856 acc_train: 0.784314 acc_val: 0.777778
epoch 44 train_time: 0.005875 loss: 0.475038 val_time: 0.001043 val_loss: 0.486832 acc_train: 0.784314 acc_val: 0.800000
epoch 45 train_time: 0.008126 loss: 0.472883 val_time: 0.001042 val_loss: 0.484342 acc_train: 0.784314 acc_val: 0.800000
epoch 46 train_time: 0.007999 loss: 0.472093 val_time: 0.000997 val_loss: 0.485877 acc_train: 0.784314 acc_val: 0.800000
epoch 47 train_time: 0.009999 loss: 0.470641 val_time: 0.002001 val_loss: 0.485934 acc_train: 0.784314 acc_val: 0.800000
epoch 48 train_time: 0.006997 loss: 0.470009 val_time: 0.000000 val_loss: 0.485674 acc_train: 0.780392 acc_val: 0.800000
epoch 49 train_time: 0.006142 loss: 0.468147 val_time: 0.001002 val_loss: 0.484136 acc_train: 0.780392 acc_val: 0.800000
epoch 50 train_time: 0.009053 loss: 0.466906 val_time: 0.002000 val_loss: 0.482787 acc_train: 0.780392 acc_val: 0.800000
epoch 51 train_time: 0.008996 loss: 0.466078 val_time: 0.001000 val_loss: 0.483676 acc_train: 0.780392 acc_val: 0.800000
epoch 52 train_time: 0.007037 loss: 0.465034 val_time: 0.001998 val_loss: 0.485045 acc_train: 0.780392 acc_val: 0.777778
epoch 53 train_time: 0.009555 loss: 0.463907 val_time: 0.001000 val_loss: 0.482525 acc_train: 0.784314 acc_val: 0.777778
epoch 54 train_time: 0.007005 loss: 0.461899 val_time: 0.001018 val_loss: 0.478441 acc_train: 0.780392 acc_val: 0.800000
epoch 55 train_time: 0.006006 loss: 0.460972 val_time: 0.001007 val_loss: 0.477887 acc_train: 0.780392 acc_val: 0.800000
epoch 56 train_time: 0.008001 loss: 0.459496 val_time: 0.001017 val_loss: 0.477387 acc_train: 0.780392 acc_val: 0.800000
epoch 57 train_time: 0.007998 loss: 0.458561 val_time: 0.001002 val_loss: 0.478509 acc_train: 0.784314 acc_val: 0.800000
epoch 58 train_time: 0.006000 loss: 0.458086 val_time: 0.001000 val_loss: 0.474418 acc_train: 0.788235 acc_val: 0.800000
epoch 59 train_time: 0.008212 loss: 0.455597 val_time: 0.001000 val_loss: 0.475687 acc_train: 0.788235 acc_val: 0.800000
epoch 60 train_time: 0.009000 loss: 0.455844 val_time: 0.001000 val_loss: 0.477320 acc_train: 0.788235 acc_val: 0.777778
epoch 61 train_time: 0.009054 loss: 0.454108 val_time: 0.001000 val_loss: 0.475539 acc_train: 0.788235 acc_val: 0.777778
epoch 62 train_time: 0.008001 loss: 0.453973 val_time: 0.000510 val_loss: 0.474032 acc_train: 0.792157 acc_val: 0.800000
epoch 63 train_time: 0.006019 loss: 0.452113 val_time: 0.001980 val_loss: 0.473794 acc_train: 0.788235 acc_val: 0.777778
epoch 64 train_time: 0.007982 loss: 0.452941 val_time: 0.001000 val_loss: 0.473315 acc_train: 0.792157 acc_val: 0.777778
epoch 65 train_time: 0.007000 loss: 0.450552 val_time: 0.001998 val_loss: 0.474471 acc_train: 0.788235 acc_val: 0.755556
epoch 66 train_time: 0.008997 loss: 0.449623 val_time: 0.000999 val_loss: 0.472488 acc_train: 0.792157 acc_val: 0.777778
epoch 67 train_time: 0.009081 loss: 0.449486 val_time: 0.000000 val_loss: 0.478104 acc_train: 0.784314 acc_val: 0.777778
epoch 68 train_time: 0.008004 loss: 0.448498 val_time: 0.001000 val_loss: 0.478637 acc_train: 0.780392 acc_val: 0.777778
epoch 69 train_time: 0.004996 loss: 0.446566 val_time: 0.001504 val_loss: 0.473761 acc_train: 0.784314 acc_val: 0.755556
epoch 70 train_time: 0.006984 loss: 0.446991 val_time: 0.000998 val_loss: 0.473666 acc_train: 0.784314 acc_val: 0.755556
epoch 71 train_time: 0.005998 loss: 0.444544 val_time: 0.000000 val_loss: 0.472638 acc_train: 0.784314 acc_val: 0.755556
epoch 72 train_time: 0.007997 loss: 0.444092 val_time: 0.001000 val_loss: 0.472773 acc_train: 0.784314 acc_val: 0.777778
epoch 73 train_time: 0.007005 loss: 0.442510 val_time: 0.000999 val_loss: 0.471294 acc_train: 0.788235 acc_val: 0.777778
epoch 74 train_time: 0.005983 loss: 0.442764 val_time: 0.000996 val_loss: 0.471654 acc_train: 0.784314 acc_val: 0.777778
epoch 75 train_time: 0.007997 loss: 0.441092 val_time: 0.001001 val_loss: 0.472774 acc_train: 0.784314 acc_val: 0.777778
epoch 76 train_time: 0.007032 loss: 0.440632 val_time: 0.002000 val_loss: 0.470745 acc_train: 0.784314 acc_val: 0.777778
epoch 77 train_time: 0.009515 loss: 0.439981 val_time: 0.002000 val_loss: 0.473636 acc_train: 0.784314 acc_val: 0.777778
epoch 78 train_time: 0.007997 loss: 0.440586 val_time: 0.001000 val_loss: 0.473777 acc_train: 0.784314 acc_val: 0.777778
epoch 79 train_time: 0.006000 loss: 0.437244 val_time: 0.001000 val_loss: 0.470391 acc_train: 0.784314 acc_val: 0.777778
epoch 80 train_time: 0.006000 loss: 0.437503 val_time: 0.002005 val_loss: 0.471904 acc_train: 0.784314 acc_val: 0.777778
epoch 81 train_time: 0.009001 loss: 0.437036 val_time: 0.002004 val_loss: 0.468702 acc_train: 0.784314 acc_val: 0.777778
epoch 82 train_time: 0.009023 loss: 0.436121 val_time: 0.000995 val_loss: 0.467339 acc_train: 0.788235 acc_val: 0.777778
epoch 83 train_time: 0.007996 loss: 0.434761 val_time: 0.000000 val_loss: 0.469654 acc_train: 0.784314 acc_val: 0.777778
epoch 84 train_time: 0.008003 loss: 0.434397 val_time: 0.001000 val_loss: 0.467646 acc_train: 0.788235 acc_val: 0.777778
epoch 85 train_time: 0.007982 loss: 0.435121 val_time: 0.000000 val_loss: 0.470189 acc_train: 0.788235 acc_val: 0.777778
epoch 86 train_time: 0.006992 loss: 0.432307 val_time: 0.002001 val_loss: 0.468117 acc_train: 0.784314 acc_val: 0.777778
epoch 87 train_time: 0.005981 loss: 0.432906 val_time: 0.002000 val_loss: 0.471442 acc_train: 0.788235 acc_val: 0.777778
epoch 88 train_time: 0.008082 loss: 0.430979 val_time: 0.001030 val_loss: 0.468135 acc_train: 0.788235 acc_val: 0.777778
epoch 89 train_time: 0.007986 loss: 0.430308 val_time: 0.001106 val_loss: 0.466767 acc_train: 0.792157 acc_val: 0.777778
epoch 90 train_time: 0.008506 loss: 0.429298 val_time: 0.002007 val_loss: 0.466248 acc_train: 0.792157 acc_val: 0.777778
epoch 91 train_time: 0.007001 loss: 0.429577 val_time: 0.001001 val_loss: 0.466661 acc_train: 0.788235 acc_val: 0.777778
epoch 92 train_time: 0.009002 loss: 0.428482 val_time: 0.002002 val_loss: 0.466210 acc_train: 0.792157 acc_val: 0.777778
epoch 93 train_time: 0.007081 loss: 0.427814 val_time: 0.001001 val_loss: 0.466178 acc_train: 0.792157 acc_val: 0.777778
epoch 94 train_time: 0.005005 loss: 0.428871 val_time: 0.001003 val_loss: 0.466175 acc_train: 0.788235 acc_val: 0.777778
epoch 95 train_time: 0.006000 loss: 0.426396 val_time: 0.001000 val_loss: 0.464582 acc_train: 0.792157 acc_val: 0.777778
epoch 96 train_time: 0.009004 loss: 0.426577 val_time: 0.001010 val_loss: 0.465821 acc_train: 0.792157 acc_val: 0.777778
epoch 97 train_time: 0.005995 loss: 0.425446 val_time: 0.002000 val_loss: 0.462678 acc_train: 0.792157 acc_val: 0.777778
epoch 98 train_time: 0.007984 loss: 0.424431 val_time: 0.000999 val_loss: 0.460735 acc_train: 0.796078 acc_val: 0.777778
epoch 99 train_time: 0.006969 loss: 0.425304 val_time: 0.002006 val_loss: 0.461348 acc_train: 0.796078 acc_val: 0.777778
epoch 100 train_time: 0.005995 loss: 0.423569 val_time: 0.000981 val_loss: 0.460811 acc_train: 0.796078 acc_val: 0.777778

6.4 Exercises and Projects

Exercise 6.1 Please hand write a report about the details of the math formulas for Logistic regression.

Exercise 6.2 CHOOSE ONE: Please use PyTorch to apply the LogisticRegression to one of the following datasets.

the iris dataset.
the dating dataset.
the titanic dataset.

Please in addition answer the following questions.

What is your accuracy score?
How many epochs do you use?
What is the batch size do you use?
Plot the learning curve (loss vs epochs, accuracy vs epochs).
Analyze the bias / variance status.