import pandas as pd
def gini(S):
N = len(S)
y = S[:, -1].reshape(N)
gini = 1 - ((pd.Series(y).value_counts()/N)**2).sum()
return gini3 Decision Trees
Given a dataset with labels, the decision tree algorithm firstly trys to split the whole dataset into two different groups, based on some speicific features. Choose which feature to use and set the threshold for the split are done.
3.1 Gini impurity
To split a dataset, we need a metric to tell whether the split is good or not. The two most popular metrics that are used are Gini impurity and Entropy. The two metrics don’t have essential differences, that the results obtained by applying each metric are very similar to each other. Therefore we will only focus on Gini impurity since it is slightly easier to compute and slightly easier to explain.
3.1.1 Motivation and Definition
Assume that we have a dataset of totally \(n\) objects, and these objects are divided into \(k\) classes. The \(i\)-th class has \(n_i\) objects. Then if we randomly pick an object, the probability to get an object belonging to the \(i\)-th class is
\[ p_i=\frac{n_i}{n} \]
If we then guess the class of the object purely based on the distribution of each class, the probability that our guess is incorrect is
\[ 1-p_i = 1-\frac{n_i}{n}. \]
Therefore, if we randomly pick an object that belongs to the \(i\)-th class and randomly guess its class purely based on the distribution but our guess is wrong, the probability that such a thing happens is
\[ p_i(1-p_i). \]
Consider all classes. The probability at which any object of the dataset will be mislabelled when it is randomly labeled is the sum of the probability described above:
\[ \sum_{i=1}^kp_i(1-p_i)=\sum_{i=1}^kp_i-\sum_{i=1}^kp_i^2=1-\sum_{i=1}^kp_i^2. \]
This is the definition formula for the Gini impurity.
Definition 3.1 The Gini impurity is calculated using the following formula
\[ Gini = \sum_{i=1}^kp_i(1-p_i)=\sum_{i=1}^kp_i-\sum_{i=1}^kp_i^2=1-\sum_{i=1}^kp_i^2, \] where \(p_i\) is the probability of class \(i\).
The way to understand Gini impurity is to consider some extreme examples.
Example 3.1 Assume that we only have one class. Therefore \(k=1\), and \(p_1=1\). Then the Gini impurity is
\[ Gini = 1-1^2=0. \] This is the minimum possible Gini impurity. It means that the dataset is pure: all the objects contained are of one unique class. In this case, we won’t make any mistakes if we randomly guess the label.
Example 3.2 Assume that we have two classes. Therefore \(k=2\). Consider the distribution \(p_1\) and \(p_2\). We know that \(p_1+p_2=1\). Therefore \(p_2=1-p_1\). Then the Gini impurity is
\[ Gini(p_1) = 1-p_1^2-p_2^2=1-p_1^2-(1-p_1)^2=2p_1-2p_1^2. \] When \(0\leq p_1\leq 1\), this function \(Gini(p_1)\) is between \(0\) and \(0.5\). - It gets \(0\) when \(p_1=0\) or \(1\). In these two cases, the dataset is still a one-class set since the size of one class is \(0\). - It gets \(0.5\) when \(p_1=0.5\). This means that the Gini impurity is maximized when the size of different classes are balanced.
3.1.2 Algorithm
Inputs A dataset \(S=\{data=[features, label]\}\) with labels.
Outputs The Gini impurity of the dataset.
Get the size \(n\) of the dataset.
Go through the label list, and find all unique labels: \(uniqueLabelList\).
Go through each label \(l\) in \(uniqueLabelList\) and count how many elements belonging to the label, and record them as \(n_l\).
Use the formula to compute the Gini impurity:
\[ Gini = 1-\sum_{l\in uniqueLabelList}\left(\frac{n_l}{n}\right)^2. \]
The sample manual codes are optional.
3.2 CART Algorithms
3.2.1 Ideas
Consider a labeled dataset \(S\) with totally \(m\) elements. We use a feature \(k\) and a threshold \(t_k\) to split it into two subsets: \(S_l\) with \(m_l\) elements and \(S_r\) with \(m_r\) elements. Then the cost function of this split is
\[ J(k, t_k)=\frac{m_l}mGini(S_l)+\frac{m_r}{m}Gini(S_r). \] It is not hard to see that the more pure the two subsets are the lower the cost function is. Therefore our goal is find a split that can minimize the cost function.
Inputs Given a labeled dataset \(S=\{[features, label]\}\).
Outputs A best split \((k, t_k)\).
- For each feature \(k\):
- For each value \(t\) of the feature:
- Split the dataset \(S\) into two subsets, one with \(k\leq t\) and one with \(k>t\).
- Compute the cost function \(J(k,t)\).
- Compare it with the current smallest cost. If this split has smaller cost, replace the current smallest cost and pair with \((k, t)\).
- For each value \(t\) of the feature:
- Return the pair \((k,t_k)\) that has the smallest cost function.
We then use this split algorithm recursively to get the decision tree.
Inputs Given a labeled dataset \(S=\{[features, label]\}\) and a maximal depth max_depth.
Outputs A decision tree.
- Starting from the original dataset \(S\). Set the working dataset \(G=S\).
- Consider a dataset \(G\). If \(Gini(G)\neq0\), split \(G\) into \(G_l\) and \(G_r\) to minimize the cost function. Record the split pair \((k, t_k)\).
- Now set the working dataset \(G=G_l\) and \(G=G_r\) respectively, and apply the above two steps to each of them.
- Repeat the above steps, until
max_depthis reached.
The manual sample code is optional.
def split(G):
m = G.shape[0]
gmini = gini(G)
pair = None
if gini(G) != 0:
numOffeatures = G.shape[1] - 1
for k in range(numOffeatures):
for t in range(m):
Gl = G[G[:, k] <= G[t, k]]
Gr = G[G[:, k] > G[t, k]]
gl = gini(Gl)
gr = gini(Gr)
ml = Gl.shape[0]
mr = Gr.shape[0]
g = gl*ml/m + gr*mr/m
if g < gmini:
gmini = g
pair = (k, G[t, k])
Glm = Gl
Grm = Gr
res = {'split': True,
'pair': pair,
'sets': (Glm, Grm)}
else:
res = {'split': False,
'pair': pair,
'sets': G}
return resFor the purpose of counting labels, we also write a code to do so.
import pandas as pd
def countlabels(S):
y = S[:, -1].reshape(S.shape[0])
labelCount = dict(pd.Series(y).value_counts())
return labelCount3.3 Decision Tree Project 1: the iris dataset
We are going to use the Decision Tree model to study the iris dataset. This dataset has already studied previously using k-NN. Again we will only use the first two features for visualization purpose.
3.3.1 Initial setup
Since the dataset will be splitted, we will put X and y together as a single variable S. In this case when we split the dataset by selecting rows, the features and the labels are still paired correctly.
We also print the labels and the feature names for our convenience.
from sklearn.datasets import load_iris
import numpy as np
iris = load_iris()
X = iris.data[:, 2:]
y = iris.target
y = y.reshape((y.shape[0],1))
S = np.concatenate([X,y], axis=1)
print(iris.target_names)
print(iris.feature_names)['setosa' 'versicolor' 'virginica']
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']3.3.2 Use package sklearn
Now we would like to use the decision tree package provided by sklearn. The process is straightforward. The parameter random_state=40 will be discussed {ref}later<note-random_state>, and it is not necessary in most cases.
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(random_state=40, min_samples_split=2)
clf.fit(X, y)DecisionTreeClassifier(random_state=40)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| criterion | 'gini' | |
| splitter | 'best' | |
| max_depth | None | |
| min_samples_split | 2 | |
| min_samples_leaf | 1 | |
| min_weight_fraction_leaf | 0.0 | |
| max_features | None | |
| random_state | 40 | |
| max_leaf_nodes | None | |
| min_impurity_decrease | 0.0 | |
| class_weight | None | |
| ccp_alpha | 0.0 | |
| monotonic_cst | None |
sklearn provide a way to automatically generate the tree view of the decision tree. The code is as follows.
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
plt.figure(figsize=(3, 3), dpi=200)
plot_tree(clf, filled=True, impurity=True, node_ids=True)[Text(0.5, 0.9166666666666666, 'node #0\nx[1] <= 0.8\ngini = 0.667\nsamples = 150\nvalue = [50, 50, 50]'),
Text(0.4090909090909091, 0.75, 'node #1\ngini = 0.0\nsamples = 50\nvalue = [50, 0, 0]'),
Text(0.4545454545454546, 0.8333333333333333, 'True '),
Text(0.5909090909090909, 0.75, 'node #2\nx[1] <= 1.75\ngini = 0.5\nsamples = 100\nvalue = [0, 50, 50]'),
Text(0.5454545454545454, 0.8333333333333333, ' False'),
Text(0.36363636363636365, 0.5833333333333334, 'node #3\nx[0] <= 4.95\ngini = 0.168\nsamples = 54\nvalue = [0, 49, 5]'),
Text(0.18181818181818182, 0.4166666666666667, 'node #4\nx[1] <= 1.65\ngini = 0.041\nsamples = 48\nvalue = [0, 47, 1]'),
Text(0.09090909090909091, 0.25, 'node #5\ngini = 0.0\nsamples = 47\nvalue = [0, 47, 0]'),
Text(0.2727272727272727, 0.25, 'node #6\ngini = 0.0\nsamples = 1\nvalue = [0, 0, 1]'),
Text(0.5454545454545454, 0.4166666666666667, 'node #7\nx[1] <= 1.55\ngini = 0.444\nsamples = 6\nvalue = [0, 2, 4]'),
Text(0.45454545454545453, 0.25, 'node #8\ngini = 0.0\nsamples = 3\nvalue = [0, 0, 3]'),
Text(0.6363636363636364, 0.25, 'node #9\nx[0] <= 5.45\ngini = 0.444\nsamples = 3\nvalue = [0, 2, 1]'),
Text(0.5454545454545454, 0.08333333333333333, 'node #10\ngini = 0.0\nsamples = 2\nvalue = [0, 2, 0]'),
Text(0.7272727272727273, 0.08333333333333333, 'node #11\ngini = 0.0\nsamples = 1\nvalue = [0, 0, 1]'),
Text(0.8181818181818182, 0.5833333333333334, 'node #12\nx[0] <= 4.85\ngini = 0.043\nsamples = 46\nvalue = [0, 1, 45]'),
Text(0.7272727272727273, 0.4166666666666667, 'node #13\ngini = 0.444\nsamples = 3\nvalue = [0, 1, 2]'),
Text(0.9090909090909091, 0.4166666666666667, 'node #14\ngini = 0.0\nsamples = 43\nvalue = [0, 0, 43]')]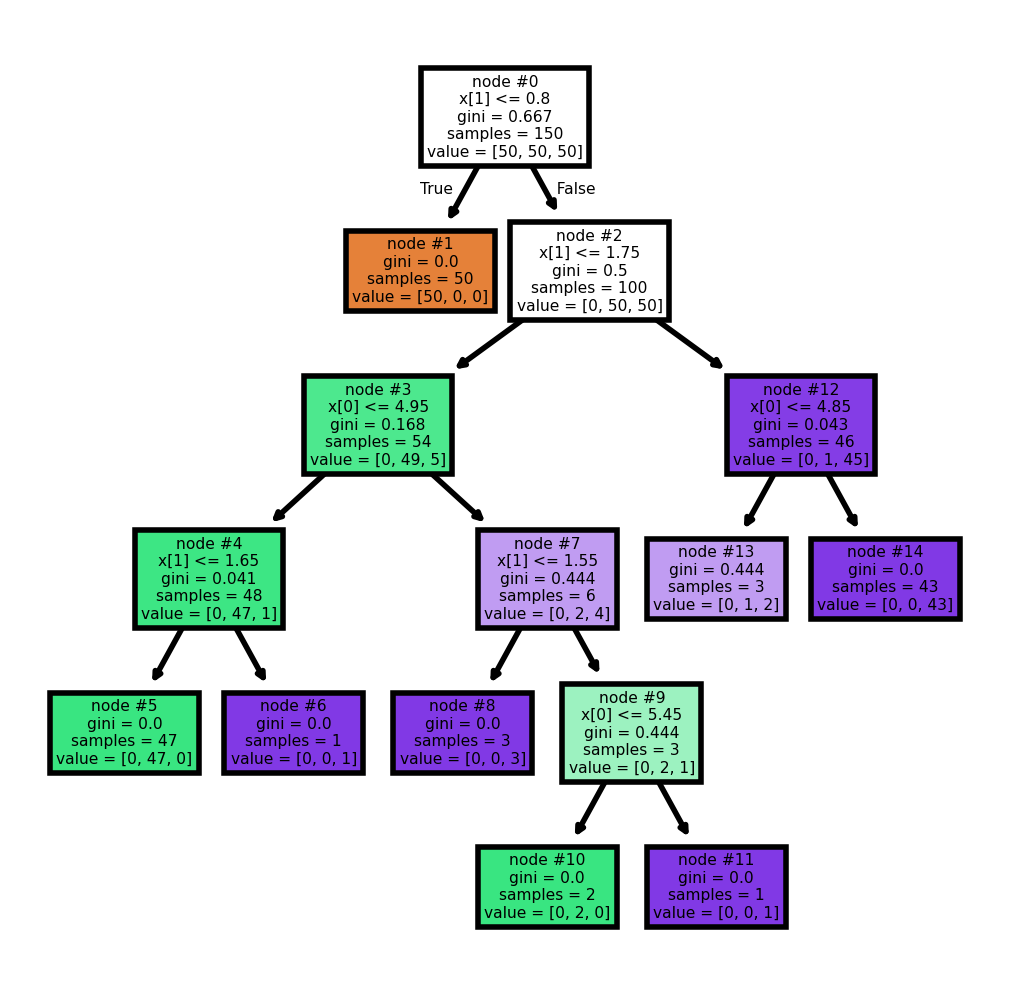
Visualize decision boundary is optional.
Similar to k-NN, we may use sklearn.inspection.DecisionBoundaryDisplay to visualize the decision boundary of this decision tree.
from sklearn.inspection import DecisionBoundaryDisplay
DecisionBoundaryDisplay.from_estimator(
clf,
X,
cmap='coolwarm',
response_method="predict",
xlabel=iris.feature_names[0],
ylabel=iris.feature_names[1],
)
# Plot the training points
plt.scatter(X[:, 0], X[:, 1], c=y, s=15)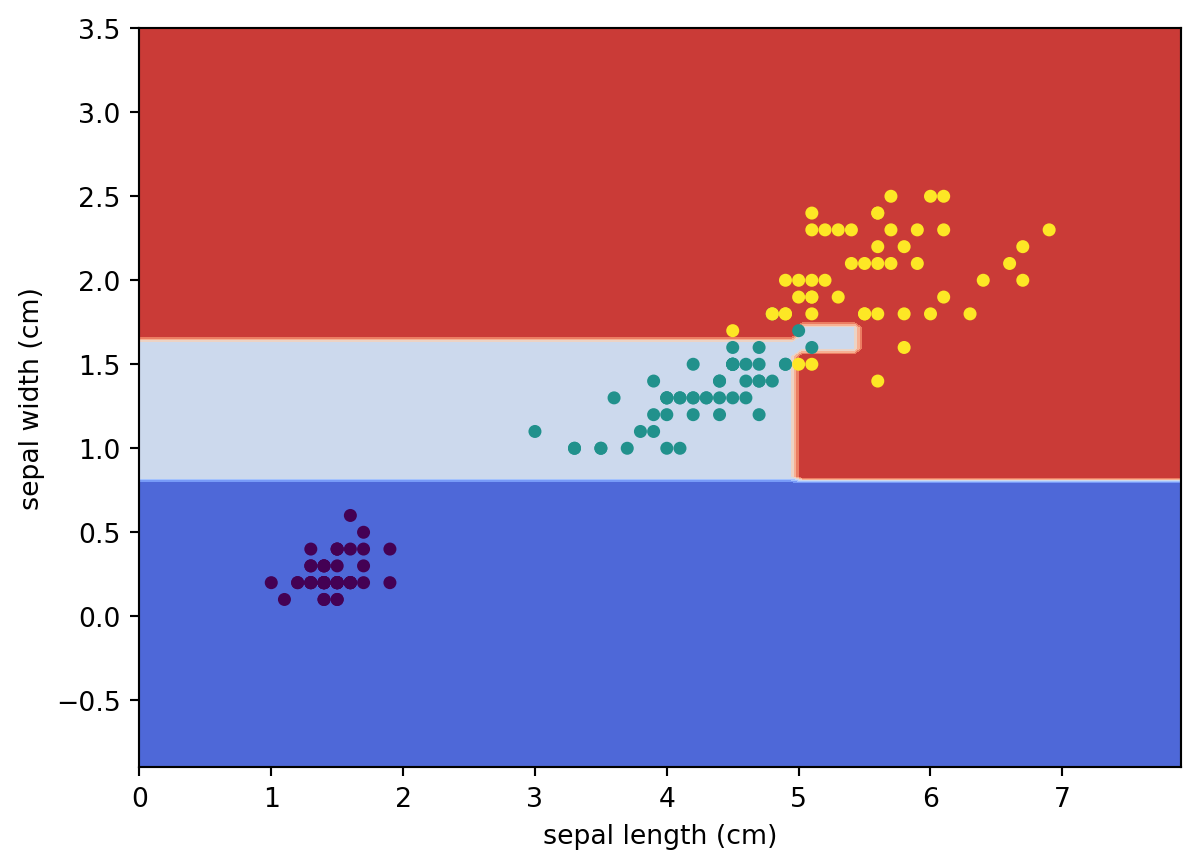
3.3.3 Tuning hyperparameters
Building a decision tree is the same as splitting the training dataset. If we are alllowed to keep splitting it, it is possible to get to a case that each end node is pure: the Gini impurity is 0. This means two things:
- The tree learns too many (unnecessary) detailed info from the training set which might not be applied to the test set. This is called overfitting. We should prevent a model from overfitting.
- We could use the number of split to indicate the progress of the learning.
In other words, the finer the splits are, the further the learning is. We need to consider some early stop conditions to prevent the model from overfitting.
Some possible early stop conditions:
max_depth: The max depth of the tree. The default isnonewhich means no limits.min_samples_split: The minimum number of samples required to split an internal node. The default is 2 which means that we will split a node with as few as 2 elements if needed.min_samples_leaf: The minimum number of samples required to be at a leaf node. The default is 1 which means that we will still split the node even if one subset only contains 1 element.
If we don’t set them (which means that we use the default setting), the dataset will be split untill all subsets are pure.
Example 3.3 (ALMOST all end nodes are pure) In this example, we let the tree grow as further as possible. It only stops when (almost) all end nodes are pure, even if the end nodes only contain ONE element (like #6 and #11).
clf = DecisionTreeClassifier(random_state=40)
clf.fit(X, y)
plt.figure(figsize=(3, 3), dpi=200)
plot_tree(clf, filled=True, impurity=True, node_ids=True)[Text(0.5, 0.9166666666666666, 'node #0\nx[1] <= 0.8\ngini = 0.667\nsamples = 150\nvalue = [50, 50, 50]'),
Text(0.4090909090909091, 0.75, 'node #1\ngini = 0.0\nsamples = 50\nvalue = [50, 0, 0]'),
Text(0.4545454545454546, 0.8333333333333333, 'True '),
Text(0.5909090909090909, 0.75, 'node #2\nx[1] <= 1.75\ngini = 0.5\nsamples = 100\nvalue = [0, 50, 50]'),
Text(0.5454545454545454, 0.8333333333333333, ' False'),
Text(0.36363636363636365, 0.5833333333333334, 'node #3\nx[0] <= 4.95\ngini = 0.168\nsamples = 54\nvalue = [0, 49, 5]'),
Text(0.18181818181818182, 0.4166666666666667, 'node #4\nx[1] <= 1.65\ngini = 0.041\nsamples = 48\nvalue = [0, 47, 1]'),
Text(0.09090909090909091, 0.25, 'node #5\ngini = 0.0\nsamples = 47\nvalue = [0, 47, 0]'),
Text(0.2727272727272727, 0.25, 'node #6\ngini = 0.0\nsamples = 1\nvalue = [0, 0, 1]'),
Text(0.5454545454545454, 0.4166666666666667, 'node #7\nx[1] <= 1.55\ngini = 0.444\nsamples = 6\nvalue = [0, 2, 4]'),
Text(0.45454545454545453, 0.25, 'node #8\ngini = 0.0\nsamples = 3\nvalue = [0, 0, 3]'),
Text(0.6363636363636364, 0.25, 'node #9\nx[0] <= 5.45\ngini = 0.444\nsamples = 3\nvalue = [0, 2, 1]'),
Text(0.5454545454545454, 0.08333333333333333, 'node #10\ngini = 0.0\nsamples = 2\nvalue = [0, 2, 0]'),
Text(0.7272727272727273, 0.08333333333333333, 'node #11\ngini = 0.0\nsamples = 1\nvalue = [0, 0, 1]'),
Text(0.8181818181818182, 0.5833333333333334, 'node #12\nx[0] <= 4.85\ngini = 0.043\nsamples = 46\nvalue = [0, 1, 45]'),
Text(0.7272727272727273, 0.4166666666666667, 'node #13\ngini = 0.444\nsamples = 3\nvalue = [0, 1, 2]'),
Text(0.9090909090909091, 0.4166666666666667, 'node #14\ngini = 0.0\nsamples = 43\nvalue = [0, 0, 43]')]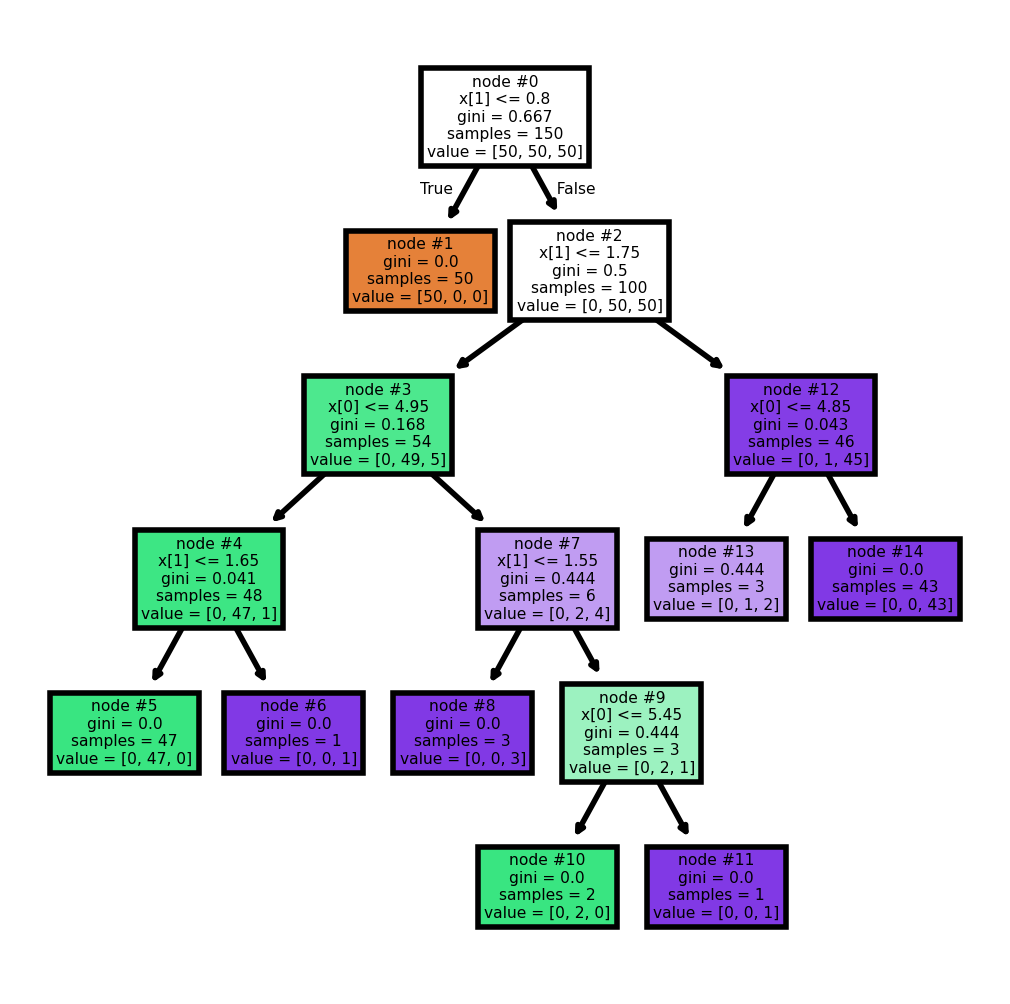
In this example there is one exception. #13 node is not pure. The reason is as follows.
X[(X[:, 0]>0.8) & (X[:, 1] >1.75) & (X[:, 0]<=4.85)]array([[4.8, 1.8],
[4.8, 1.8],
[4.8, 1.8]])All the data points in this node has the same feature while their labels are different. They cannot be split further purely based on features.
Therefore we could treat these hyperparameters as an indicator about how far the dataset is split. The further the dataset is split, the further the learning goes, the more details are learned. Since we don’t want the model to be overfitting, we don’t want to split the dataset that far. In this case, we could use the learning curve to help us make the decision.
In this example, let us choose min_samples_leaf as the indicator. When min_samples_leaf is big, the learning just starts. When min_samples_leaf=1, we reach the far most side of learning. We will see how the training and testing accuracy changes along the learning process.
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=42)
num_leaf = list(range(1, 100))
train_acc = []
test_acc = []
for i in num_leaf:
clf = DecisionTreeClassifier(random_state=42, min_samples_leaf=i)
clf.fit(X_train, y_train)
train_acc.append(clf.score(X_train, y_train))
test_acc.append(clf.score(X_test, y_test))
plt.plot(num_leaf, train_acc, label='training')
plt.plot(num_leaf, test_acc, label='testing')
plt.gca().set_xlim((max(num_leaf)+1, min(num_leaf)-1))
plt.legend()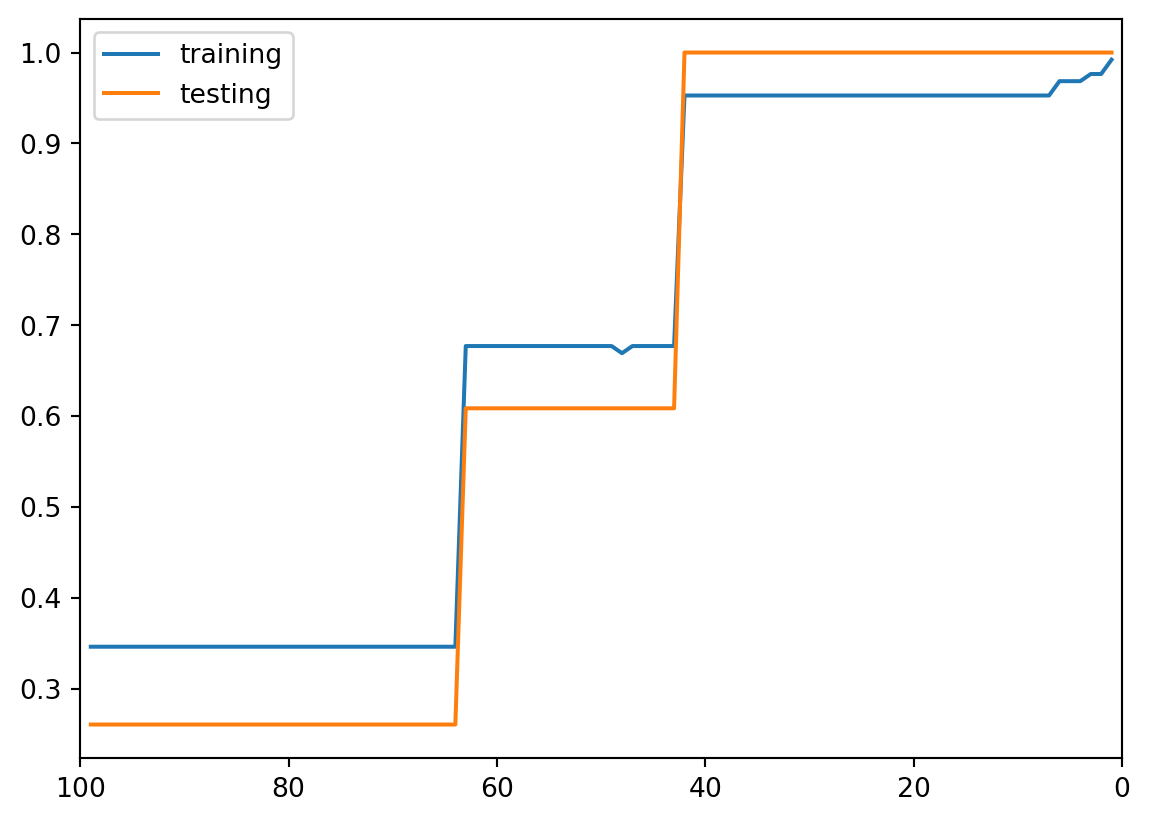
From this plot, the accuracy has a big jump at min_sample_leaf=41. So we could choose this to be our hyperparameter.
3.3.4 Apply CART manually (optional)
The manual sample code is optional.
We apply split to the dataset S.
from assests.codes.dt import gini, split, countlabels
r = split(S)
if r['split'] is True:
Gl, Gr = r['sets']
print(r['pair'])
print('The left subset\'s Gini impurity is {g:.2f},'.format(g=gini(Gl)),
' and its label counts is {d:}'.format(d=countlabels(Gl)))
print('The right subset\'s Gini impurity is {g:.2f},'.format(g=gini(Gr)),
' and its label counts is {d}'.format(d=countlabels(Gr)))(0, np.float64(1.9))
The left subset's Gini impurity is 0.00, and its label counts is {0.0: np.int64(50)}
The right subset's Gini impurity is 0.50, and its label counts is {1.0: np.int64(50), 2.0: np.int64(50)}The results shows that S is splitted into two subsets based on the 0-th feature and the split value is 1.9.
The left subset is already pure since its Gini impurity is 0. All elements in the left subset is label 0 (which is setosa). The right one is mixed since its Gini impurity is 0.5. Therefore we need to apply split again to the right subset.
r = split(Gr)
if r['split'] is True:
Grl, Grr = r['sets']
print(r['pair'])
print('The left subset\'s Gini impurity is {g:.2f},'.format(g=gini(Grl)),
' and its label counts is {d:}'.format(d=countlabels(Grl)))
print('The right subset\'s Gini impurity is {g:.2f},'.format(g=gini(Grr)),
' and its label counts is {d}'.format(d=countlabels(Grr)))(1, np.float64(1.7))
The left subset's Gini impurity is 0.17, and its label counts is {1.0: np.int64(49), 2.0: np.int64(5)}
The right subset's Gini impurity is 0.04, and its label counts is {2.0: np.int64(45), 1.0: np.int64(1)}This time the subset is splitted into two more subsets based on the 1-st feature and the split value is 1.7. The total Gini impurity is minimized using this split.
The decision we created so far can be described as follows:
- Check the first feature
sepal length (cm)to see whether it is smaller or equal to1.9.- If it is, classify it as lable
0which issetosa. - If not, continue to the next stage.
- If it is, classify it as lable
- Check the second feature
sepal width (cm)to see whether it is smaller or equal to1.7.- If it is, classify it as label
1which isversicolor. - If not, classify it as label
2which isvirginica.
- If it is, classify it as label
3.3.4.1 Analyze the differences between the two methods
The tree generated by sklearn and the tree we got manually is a little bit different. Let us explore the differences here.
To make it easier to split the set, we could convert the numpy.ndarray to pandas.DataFrame.
import pandas as pd
df = pd.DataFrame(X)
df.head()| 0 | 1 | |
|---|---|---|
| 0 | 1.4 | 0.2 |
| 1 | 1.4 | 0.2 |
| 2 | 1.3 | 0.2 |
| 3 | 1.5 | 0.2 |
| 4 | 1.4 | 0.2 |
Now based on our tree, we would like to get all data points that the first feature (which is marked as 0) is smaller or equal to 1.9. We save it as df1. Similarly based on the tree gotten from sklearn, we would like to get all data points taht the second feature (which is marked as 1) is smaller or equal to 0.8 and save it to df2.
df1 = df[df[0]<=1.9]
df2 = df[df[1]<=0.8]Then we would like to compare these two dataframes. What we want is to see whether they are the same regardless the order. One way to do this is to sort the two dataframes and then compare them directly.
To sort the dataframe we use the method DataFrame.sort_values. The details can be found here. Note that after sort_values we apply reset_index to reset the index just in case the index is massed by the sort operation.
Then we use DataFrame.equals to check whether they are the same.
df1sorted = df1.sort_values(by=df1.columns.tolist()).reset_index(drop=True)
df2sorted = df2.sort_values(by=df2.columns.tolist()).reset_index(drop=True)
print(df1sorted.equals(df2sorted))TrueSo these two sets are really the same. The reason this happens can be seen from the following two graphs.
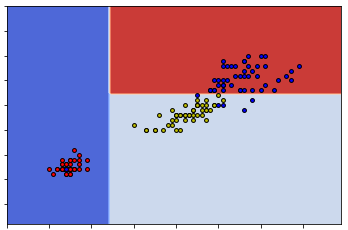
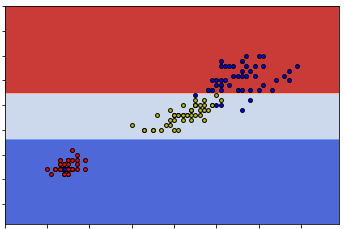
sklearnSo you can see that either way can give us the same classification. This means that given one dataset the construction of the decision tree might be random at some points.
Since the split is random, when using sklearn.DecisionTreeClassifier to construct decision trees, sometimes we might get the same tree as what we get from our naive codes.
To illustrate this phenomenaon I need to set the random state in case it will generate the same tree as ours when I need it to generate a different tree. The parameter random_state=40 mentioned before is for this purpose.
Another difference is the split value of the second branch. In our case it is 1.7 and in sklearn case it is 1.75. So after we get the right subset from the first split (which is called dfr), we would split it into two sets based on whether the second feature is above or below 1.7.
dfr = df[df[0]>1.9]
df2a = dfr[dfr[1]>1.7]
df2b = dfr[dfr[1]<=1.7]
print(df2b[1].max())
print(df2a[1].min())1.7
1.8Now you can see where the split number comes from. In our code, when we found a split, we will directly use that number as the cut. In this case it is 1.7.
In sklearn, when it finds a split, the algorithm will go for the middle of the gap as the cut. In this case it is (1.7+1.8)/2=1.75.
3.3.5 Pruning
Other than tuning hyperparameters, we also want to prune our tree in order to reduce overfitting further. The pruning algorithm introduced together with CART is called Minimal-Cost-Complexity Pruning (MCCP).
The idea is to use the cost-complexity measure to replace Gini impurity to grow the tree. The cost-complexity measure is gotten by adding the total number of end nodes with the coefficent ccp_alpha to the Gini impurity. The parameter ccp_alpha>=0 is known as the complexity parameter, and it can help the tree to self-balance the number of end nodes and the Gini impurity.
In sklearn, we use cost_complexity_pruning_path to help us find the effective alphas and the corresponding impurities.
clf = DecisionTreeClassifier(random_state=42)
ccp_path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = ccp_path.ccp_alphas, ccp_path.impuritiesThe list ccp_alphas contains all important ccp_alphas. We could train a model for each of them. We could use the argument ccp_alpha to control the value when initialize the model. After we train all these tree models for each effective ccp_alpha, we evaluate the model and record the results.
clfs = []
for ccp_alpha in ccp_alphas:
clf = DecisionTreeClassifier(random_state=42, ccp_alpha=ccp_alpha)
clf.fit(X_train, y_train)
clfs.append(clf)
node_counts = [clf.tree_.node_count for clf in clfs]
depth = [clf.tree_.max_depth for clf in clfs]
train_acc = [clf.score(X_train, y_train) for clf in clfs]
test_acc = [clf.score(X_test, y_test) for clf in clfs]We would like to visualize these info.
fig, ax = plt.subplots(3, 1)
ax[0].plot(ccp_alphas, node_counts, marker="o", drawstyle="steps-post")
ax[0].set_xlabel("alpha")
ax[0].set_ylabel("number of nodes")
ax[1].plot(ccp_alphas, depth, marker="o", drawstyle="steps-post")
ax[1].set_xlabel("alpha")
ax[1].set_ylabel("depth of tree")
ax[2].plot(ccp_alphas, train_acc, marker="o", drawstyle="steps-post", label='train')
ax[2].plot(ccp_alphas, test_acc, marker="o", drawstyle="steps-post", label='test')
ax[2].set_xlabel("alpha")
ax[2].set_ylabel("accuracy")
ax[2].legend()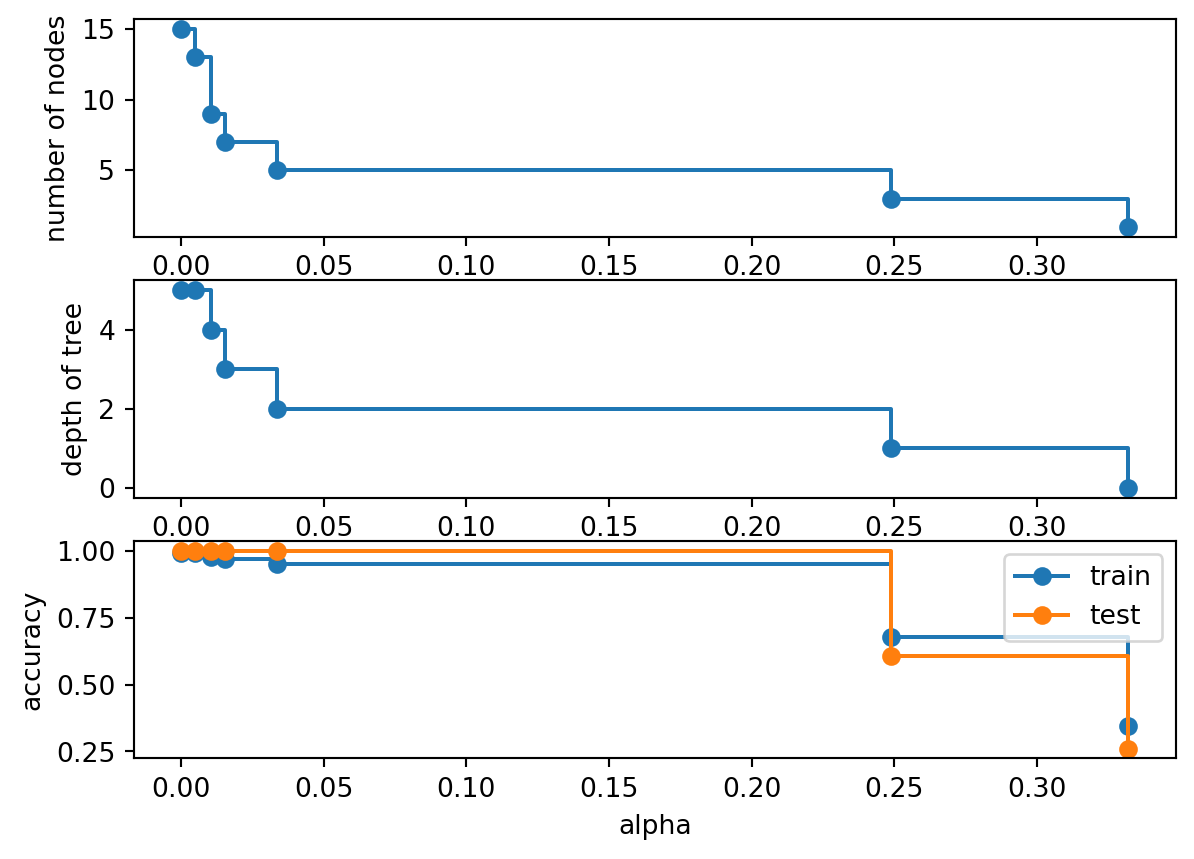
Based on the plot, it seems that the fourth dot 0.01534424 is a good fit. So this is the complexity parameter we are going to use.
We could combine all the code above into a function.
from sklearn.base import clone
def eval_ccp_alphas(clf, X, y):
ccp_path = clf.cost_complexity_pruning_path(X, y)
ccp_alphas, impurities = ccp_path.ccp_alphas, ccp_path.impurities
clfs = []
for ccp_alpha in ccp_alphas:
clf_tmp = clone(clf)
clf_tmp.set_params(ccp_alpha=ccp_alpha)
clf_tmp.fit(X, y)
clfs.append(clf_tmp)
node_counts = [clf.tree_.node_count for clf in clfs]
depth = [clf.tree_.max_depth for clf in clfs]
train_acc = [clf.score(X_train, y_train) for clf in clfs]
test_acc = [clf.score(X_test, y_test) for clf in clfs]
fig, ax = plt.subplots(3, 1)
ax[0].plot(ccp_alphas, node_counts, marker="o", drawstyle="steps-post")
ax[0].set_xlabel("alpha")
ax[0].set_ylabel("number of nodes")
ax[1].plot(ccp_alphas, depth, marker="o", drawstyle="steps-post")
ax[1].set_xlabel("alpha")
ax[1].set_ylabel("depth of tree")
ax[2].plot(ccp_alphas, train_acc, marker="o", drawstyle="steps-post", label='train')
ax[2].plot(ccp_alphas, test_acc, marker="o", drawstyle="steps-post", label='test')
ax[2].set_xlabel("alpha")
ax[2].set_ylabel("accuracy")
ax[2].legend()
return ccp_alphaseval_ccp_alphas(DecisionTreeClassifier(random_state=42), X_train, y_train)array([0. , 0.00485564, 0.01049869, 0.01534424, 0.03364964,
0.24888323, 0.33214852])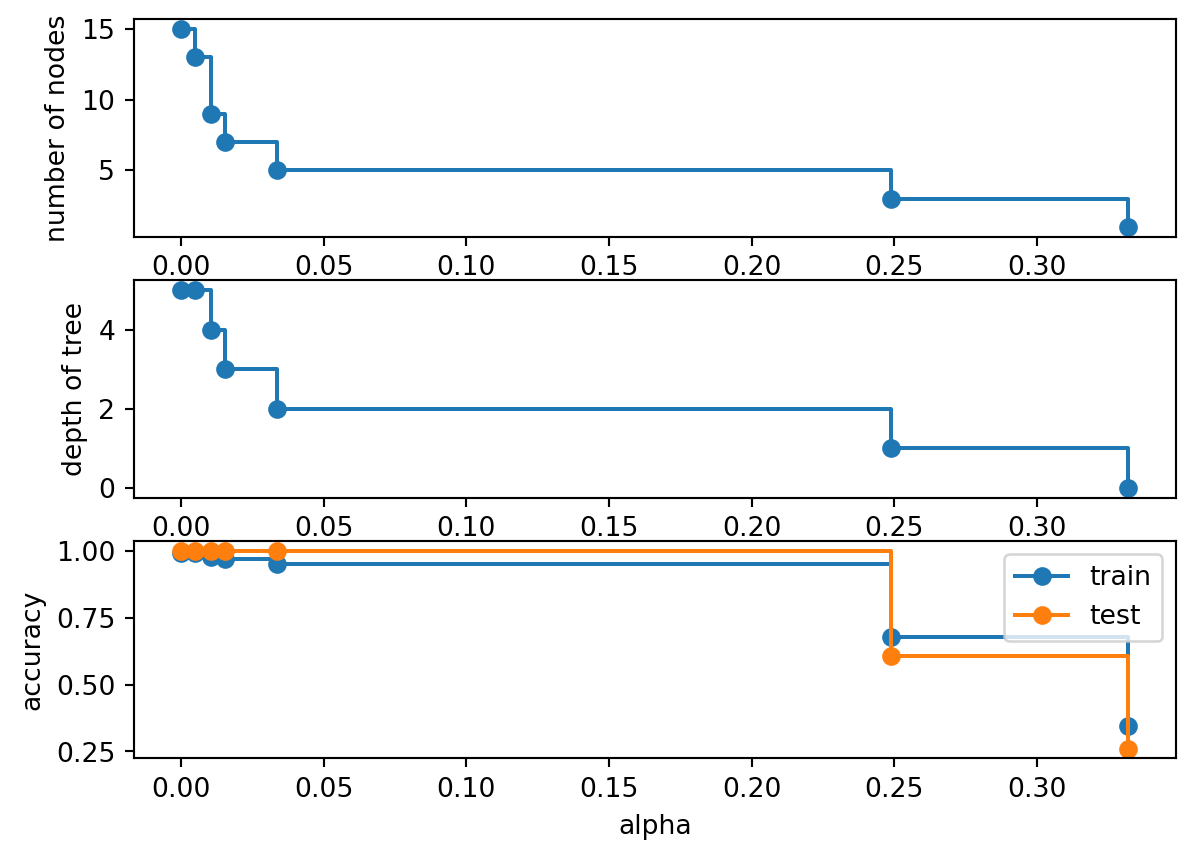
3.4 Exercises and Projects
Exercise 3.1 The dataset and its scattering plot is given below.
- Please calculate the Gini impurity of the whole set by hand.
- Please apply CART to create the decision tree by hand.
- Please use the tree you created to classify the following points:
- \((0.4, 1.0)\)
- \((0.6, 1.0)\)
- \((0.6, 0)\)
The following code is for ploting. You may also get the precise data points by reading the code. You don’t need to write codes to solve the problem.
import pandas as pd
import matplotlib.pyplot as plt
data = {'x0': [0.22, 0.37, 0.42, 0.45, 0.18, 0.20, 0.21, 0.23, 0.35, 0.58,
0.60, 0.61, 0.62, 0.65, 0.70, 0.75, 0.82, 0.88, 0.90, 0.92],
'x1': [0.83, 0.78, 0.65, 0.37, 0.57, 0.45, 0.67, 0.22, 0.43, 0.33,
0.75, 0.50, 0.21, 0.31, 0.64, 0.70, 0.80, 0.82, 0.61, 0.81],
'y': ['r', 'r', 'b', 'r', 'r', 'r', 'r', 'r', 'r', 'r',
'b', 'b', 'r', 'r', 'b', 'r', 'r', 'r', 'r', 'r']}
df = pd.DataFrame(data)
plt.figure(figsize=(7, 7))
plt.scatter(df['x0'], df['x1'], c=df['y'])
_ = plt.xlim(0, 1)
_ = plt.ylim(0, 1)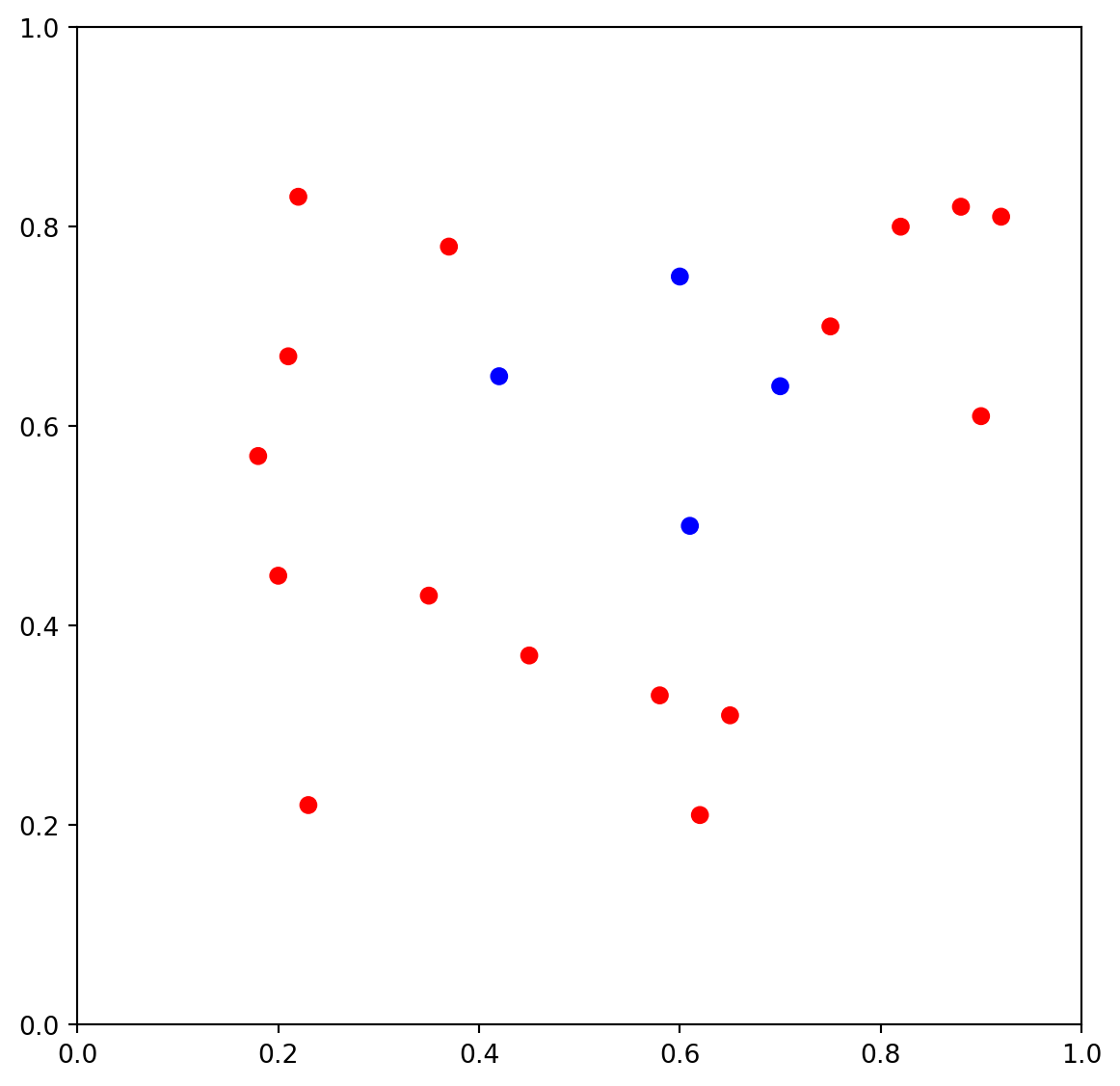
Exercise 3.2 CHOOSE ONE: Please apply the Decision Tree to one of the following datasets.
- dating dataset (in Chpater 2).
- the
titanicdataset.
Please answer the following questions.
- Please find the best hyperparameters of your choice.
- Please record the accuracy (or cross-validation score) of your model and compare it with the models you learned before (kNN).
- Please find the two most important features and explane your reason.