3  Package: numpy

The main reference for this chapter is [1].

3.1 Basics

The basic data structure for numpy is numpy.ndarray. You may treat it as a generalized version of lists. However it can do so much more than the build-in list.

To use numpy, we just import it. In most cases you would like to use the alias np.

import numpy as np
Note

In many cases, numpy.ndarray is a huge object since it stores tons of data. Therefore many of the operations related to numpy.ndarray are “in-place” by default. This means that if you don’t explicitly ask for a copy, there will be only one copy of the array and all later operations make changes to the original one.

However there are many cases that

3.2 Create np.ndarray

  • convert a list into a numpy array.
  • np.zeros, np.zeros_like
  • np.ones, np.ones_like
  • np.eye
  • np.random.rand
  • np.arange
  • np.linspace
Note

Please be very careful about the format of the input. For example, when you want to specify the dimension of the array, using np.zeros, you need to input a tuple. On the other hand, when using np.random.rand, you just directly input the dimensions one by one.

import numpy as np

np.zeros((3, 2))
np.random.rand(3, 2)

In this case, the official documents are always your friend.

3.3 Mathematical and Statistical Methods

  • +, -, *, /, **, etc..

  • np.sin, np.exp, np.sqrt, etc..

  • mean, sum, std, var, cumsum

  • max and min

  • maximum and minimum

  • argmin and argmax

  • np.sort

  • np.unique, np.any

  • np.dot: Matrix multiplication

  • np.concatenate

  • Broadcast

Example 3.1 (Axis) Given A = np.array([[1,2],[3,4]]) and B = np.array([[5,6],[7,8]]), please use np.concatenate to concatencate these two matrices to get a new matrix, in the order:

  • A left, B right
  • A right, B left
  • A up, B down
  • A down, B up

3.4 Common attributes and methods

  • shape
  • dtype
  • ndim
  • Any arithmetic operations between equal-size arrays applies the operation element-wise.

Example 3.2 MNIST is a very famous dataset of hand written images. Here is how to load it. Note that in this instance of the dataset the data are stored as numpy arraies.

import tensorflow as tf

(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train.shape

3.5 Basic indexing and slicing

First see the following example.

Example 3.3  

import numpy as np
arr = np.arange(10)

print(arr[5])
print(arr[5:8])

arr[5:8] = 12
print(arr)

print(arr[5:8:2])
print(arr[8:5:-1])
print(arr[::-1])
5
[5 6 7]
[ 0  1  2  3  4 12 12 12  8  9]
[12 12]
[ 8 12 12]
[ 9  8 12 12 12  4  3  2  1  0]

To do slicing in higher dimensional case, you may either treat a numpy array as a nested list, or you may directly work with it with multiindexes.

Example 3.4  

import numpy as np
arr3d = np.arange(12).reshape(2, 2, 3)

print('case 1:\n {}'.format(arr3d))
print('case 2:\n {}'.format(arr3d[0, 1, 2]))
print('case 3:\n {}'.format(arr3d[:, 0: 2, 1]))
print('case 4:\n {}'.format(arr3d[:, 0: 2, 1:2]))
case 1:
 [[[ 0  1  2]
  [ 3  4  5]]

 [[ 6  7  8]
  [ 9 10 11]]]
case 2:
 5
case 3:
 [[ 1  4]
 [ 7 10]]
case 4:
 [[[ 1]
  [ 4]]

 [[ 7]
  [10]]]

3.6 Boolean Indexing

numpy array can accept index in terms of numpy arries with boolean indexing.

Example 3.5  

import numpy as np
a = np.arange(4)
b = np.array([True, True, False, True])
print(a)
print(b)
print(a[b])
[0 1 2 3]
[ True  True False  True]
[0 1 3]

We could combine this way with the logic computation to filter out the elements we don’t want.

Example 3.6 Please replace the odd number in the array by its negative.

import numpy as np
arr = np.arange(10)
odd = arr %2 == 1
arr[odd] = arr[odd] * (-1)

print(arr)
[ 0 -1  2 -3  4 -5  6 -7  8 -9]

3.7 Fancy indexing

Fancy indexing is a term adopted by NumPy to describe indexing using integer arrays.

Example 3.7  

import numpy as np

arr = np.zeros((8, 4))
for i in range(8):
    arr[i] = i

arr[[4, 3, 0, 6]]
array([[4., 4., 4., 4.],
       [3., 3., 3., 3.],
       [0., 0., 0., 0.],
       [6., 6., 6., 6.]])

Example 3.8  

import numpy as np

arr = np.arange(32).reshape((8, 4))
print(arr)
print(arr[[1, 5, 7, 2], [0, 3, 1, 2]])
print(arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]])
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]
 [16 17 18 19]
 [20 21 22 23]
 [24 25 26 27]
 [28 29 30 31]]
[ 4 23 29 10]
[[ 4  7  5  6]
 [20 23 21 22]
 [28 31 29 30]
 [ 8 11  9 10]]

3.8 Copies and views

The view of an numpy array is a way to get access to the array without copying internel data. When operating with a view, the original data as well as all other views of the original data will be modified simutanously.

The default setting for copies and views is that, basic indexing and slicing will make views, and advanced indexing and slicing (e.g. boolean indexing, fancy indexing, etc.) will make copies. For other operations, you need to check the documents to know how they work. For example, np.reshape creates a view where possible, and np.flatten always creates a copy.

You may use np.view() or np.copy() to make views or copies explicitly. ::: {#exm-}

import numpy as np
arr = np.arange(10)
b = arr[5:8]
print('arr is {}'.format(arr))
print('b is {}'.format(b))

b[0] = -1
print('arr is {}'.format(arr))
print('b is {}'.format(b))


arr[6] = -2
print('arr is {}'.format(arr))
print('b is {}'.format(b))

print('The base of b is {}'.format(b.base))
arr is [0 1 2 3 4 5 6 7 8 9]
b is [5 6 7]
arr is [ 0  1  2  3  4 -1  6  7  8  9]
b is [-1  6  7]
arr is [ 0  1  2  3  4 -1 -2  7  8  9]
b is [-1 -2  7]
The base of b is [ 0  1  2  3  4 -1 -2  7  8  9]

:::

The way to make explicit copy is .copy().

Example 3.9  

import numpy as np
arr = np.arange(10)
b = arr[5:8].copy()
print('arr is {}'.format(arr))
print('b is {}'.format(b))

b[0] = -1
print('arr is {}'.format(arr))
print('b is {}'.format(b))


arr[6] = -2
print('arr is {}'.format(arr))
print('b is {}'.format(b))

print('The base of b is {}'.format(b.base))
arr is [0 1 2 3 4 5 6 7 8 9]
b is [5 6 7]
arr is [0 1 2 3 4 5 6 7 8 9]
b is [-1  6  7]
arr is [ 0  1  2  3  4  5 -2  7  8  9]
b is [-1  6  7]
The base of b is None

3.9 More commands

  • .T
  • axis=n is very important.
  • np.reshape()
  • np.tile()
  • np.repeat()

3.10 More advanced commands

  • np.where()
  • np.any()
  • np.all()
  • np.argsort()

Example 3.10 Get the position where elements of a and b match.

a = np.array([1,2,3,2,3,4,3,4,5,6])
b = np.array([7,2,10,2,7,4,9,4,9,8])

np.where(a == b)
(array([1, 3, 5, 7], dtype=int64),)

Example 3.11  

a = np.array([1,2,3,2,3,4,3,4,5,6])
b = np.array([7,2,10,2,7,4,9,4,9,8])

np.where(a == b, a*2, b+1)
array([ 8,  4, 11,  4,  8,  8, 10,  8, 10,  9])

Example 3.12 (Playing with axis)  

import numpy as np
a = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])

np.any(a==1, axis=0)
np.any(a==1, axis=1)
np.any(a==1, axis=2)


np.any(a==2, axis=0)
np.any(a==2, axis=1)
np.any(a==2, axis=2)

np.any(a==5, axis=0)
np.any(a==5, axis=1)
np.any(a==5, axis=2)
array([[False, False],
       [ True, False]])

3.11 Examples

Example 3.13 (Random walks) Adam walks randomly along the axis. He starts from 0. Every step he has equal possibility to go left or right. Please simulate this process.

Use choices to record the choice of Adam at each step. We may generate a random array where 0 represents left and 1 represents right.

Use positions to record the position of Adam at each step. Using choices, the position is +1 if we see a 1 and the position is -1 if we see a 0. So the most elegent way to perform this is to

  1. Convert choices from {0, 1} to {-1, 1}.
  2. To record the starting position, we attach 0 to the beginning of the new choices.
  3. Apply cumsum to choices to get positions.
import numpy as np

step = 30
choices = np.random.randint(2, size=step)
choices = choices * 2 - 1
choices = np.concatenate(([0], choices))
positions = choices.cumsum()

import matplotlib.pyplot as plt
plt.plot(positions)

Example 3.14 (Many random walks) We mainly use numpy.ndarray to write the code in the previous example. The best part here is that it can be easily generalized to many random walks.

Still keep choices and positions in mind. Now we would like to deal with multiple people simutanously. Each row represents one person’s random walk. All the formulas stay the same. We only need to update the dimension setting in the previous code.

  • Update size in np.random.randint.
  • Update [0] to np.zeros((N, 1)) in concatenate.
  • For cumsum and concatenate, add axis=1 to indicate that we perform the operations along axis 1.
  • We plot each row in the same figure. plt.legend is used to show the label for each line.
import numpy as np

step = 30
N = 3
choices = np.random.randint(2, size=(N, step))
choices = choices * 2 - 1
choices = np.concatenate((np.zeros((N, 1)), choices), axis=1)
positions = choices.cumsum(axis=1)

import matplotlib.pyplot as plt
for row in positions:
    plt.plot(row)
plt.legend([1, 2, 3])
<matplotlib.legend.Legend at 0x1fc2c4f5940>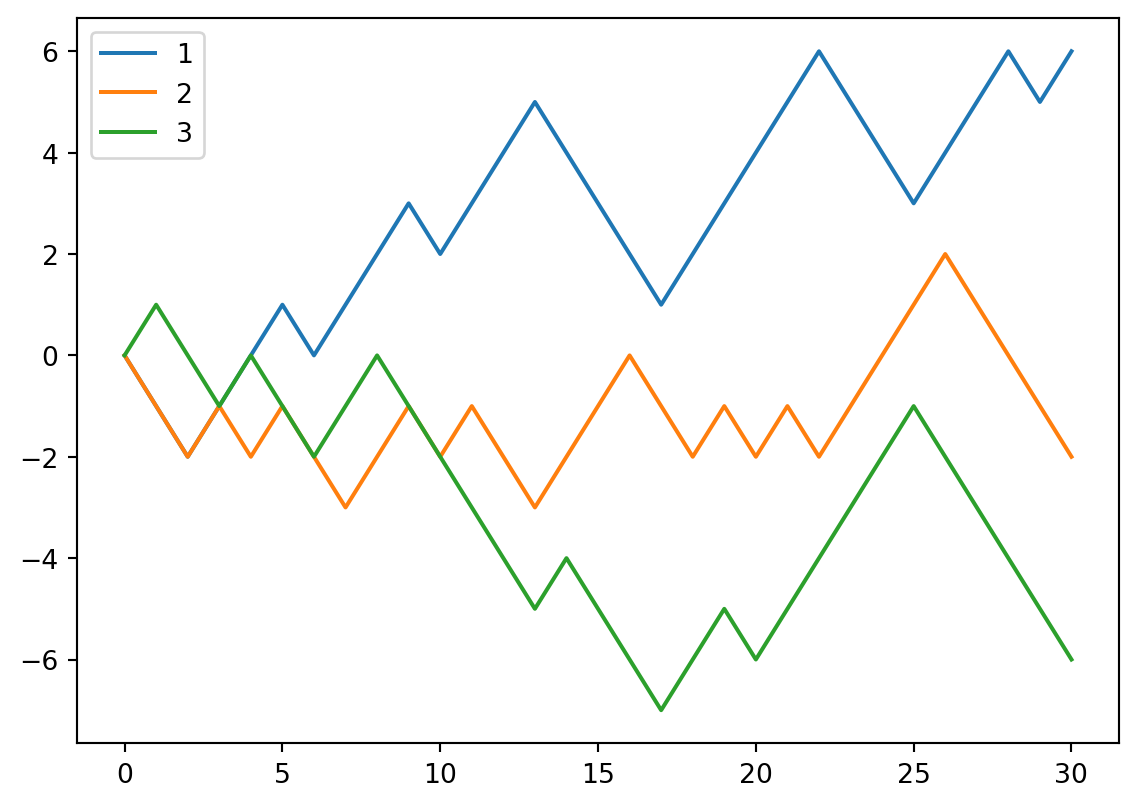

Example 3.15 (Analyze positions) We play with the numpy array positions to get some information about the random walks of three generated in the previous example.

  • The maximal position:
positions.max()
6.0
  • The maximal position for each one:
positions.max(axis=1)
array([6., 2., 1.])
  • The maximal position across all three for each step:
positions.max(axis=0)
array([ 0.,  1.,  0., -1.,  0.,  1.,  0.,  1.,  2.,  3.,  2.,  3.,  4.,
        5.,  4.,  3.,  2.,  1.,  2.,  3.,  4.,  5.,  6.,  5.,  4.,  3.,
        4.,  5.,  6.,  5.,  6.])
  • Check whether anyone once got to the position 3:
(positions>=3).any(axis=1)
array([ True, False, False])
  • The number of people who once got to the position 3:
(positions>=3).any(axis=1).sum()
1
  • Which step for each one gets to the right most position:
positions.argmax(axis=1)
array([22, 26,  1], dtype=int64)

3.12 Exercises

Many exercises are from [2].

Exercise 3.1 (array) Write a NumPy program to create a \(3\times3\) matrix with values ranging from 2 to 10.

Exercise 3.2 (array) Write a NumPy program to create a null vector of size 10 and update sixth value to 11.

Exercise 3.3 (array) Write a NumPy program to reverse an array (first element becomes last).

Exercise 3.4 (array) Write a NumPy program to create a \(10\times10\) 2D-array with 1 on the border and 0 inside.

Exercise 3.5 (repeat and tile) Given a = np.array([1,2,3]), please get the desired output array([1, 1, 1, 2, 2, 2, 3, 3, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3]).

Exercise 3.6 (Compare two numpy arraies) Consider two numpy arraies x and y. Compare them entry by entry. We would like to know how many are the same.

Click to expand.

Solution. Note that bool values True and False can be treated as numbers 1 and 0.

import numpy as np

x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 1, 4, 4, 5])

numofsame = np.sum(x == y)
print(numofsame)
2

Exercise 3.7 Get all items between 5 and 10 from an array a = np.array([2, 6, 1, 9, 10, 3, 27]).

Exercise 3.8 Swap rows 1 and 2 in the array arr = np.arange(9).reshape(3,3).

Exercise 3.9 Please finish the following tasks.

  1. Reverse the rows of a 2D array arr = np.arange(9).reshape(3,3).
  2. Reverse the columns of a 2D array arr = np.arange(9).reshape(3,3).

Exercise 3.10 Create a 2D array of shape 5x3 to contain random decimal numbers between 5 and 10.

Exercise 3.11 Use the following code to get the dataset iris.

import numpy as np

url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_1d = np.genfromtxt(url, delimiter=',', dtype=None, encoding=None)

  1. iris_1d is a 1D numpy array that each item is a tuple. Please construct a new 1D numpy array that each item is the last componenet of each tuple in iris_1d.

  2. Convert iris_1d into a 2D array iris_2d by omitting the last field of each item.

Exercise 3.12 (Normalization) Use the following code to get an 1D array sepallength.

import numpy as np

url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0],
                            encoding=None)

Please normalize it such that the values of each item is between 0 and 1.

Exercise 3.13 np.isnan() is a function to check whether each entry of a numpy array is nan or not. Please use this as well as np.where to find all nan entries in an array.

You may use the following array iris_2d to test your code.

import numpy as np
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', encoding=None)
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan

Exercise 3.14 Select the rows of iris_2d that does not have any nan value.

import numpy as np
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3],
                        encoding=None)
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan

Exercise 3.15 Replace all nan with 0 in numpy array iris_2d.

import numpy as np
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3],
                        encoding=None)
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan

Exercise 3.16 Consider x = np.array([1, 2, 1, 1, 3, 4, 3, 1, 1, 2, 1, 1, 2]). Please find the index of 5th repetition of number 1 in x.

3.13 Projects

Exercise 3.17 (Adding one axis) Please download this file.

  1. Please use matplotlib.pyplot.imread() to read the file as a 3D numpy array.
  2. Check the shape of the array.
  3. Add one additional axis to it as axis 0 to make it into a 4D array.

Exercise 3.18 (Random) Please finish the following tasks.

  1. Use the package np.random to flip a coin 100 times and record the result in a list coin.
  2. Assume that the coin is not fair, and the probability to get H is p. Write a code to flip the coin 100 times and record the result in a list coin, with a given parameter p. You may use p=.4 as the first choice.
  3. For each list coin created above, write a code to find the longest H streak. We only need the biggest number of consecutive H we get during this 100 tosses. It is NOT necessary to know when we start the streak.
Click for Hint.

Solution. The following ideas can be used to solve the problem.

  • np.where
  • string, split and join

Exercise 3.19 (Bins) Please read the document of np.digitize, and use it to do the following task.

Set the following bins:

  • Less than 3: small
  • 3-5: medium
  • Bigger than 5: large

Please transform the following data iris_2c into texts using the given bins.

import numpy as np
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2c = np.genfromtxt(url, delimiter=',', dtype='object')[:, 2].astype('float')

Exercise 3.20 Consider a 2D numpy array a.

import numpy as np
a = np.random.rand(5, 5)
  1. Please sort it along the 3rd column.
  2. Please sort it along the 2nd row.
Click for Hint.

Solution. Please use np.argsort for the problem.

Exercise 3.21 (One-hot vector) Compute the one-hot encodings of a given array. You may use the following array as a test example. In this example, there are 3 labels. So the one-hot vectors are 3 dimensional vectors.

For more infomation about one-hot encodings, you may check the Wiki page. You are not allowed to use packages that can directly compute the one-hot encodings for this problem.

import numpy as np
arr = np.random.randint(1,4, size=6)

Exercise 3.22 From the given 1d array arr = np.arange(15), generate a 2d matrix using strides, with a window length of 4 and strides of 2, like [[0,1,2,3], [2,3,4,5], [4,5,6,7]..].